- Home
- /
- Analytics
- /
- Stat Procs
- /
- Re: Likelihood Ratio Test in Mixed Model - Proc Mixed
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You misunderstand the method. Yes, the two models have the same number of parameters associated with random effects (variances or covariances), but they have different numbers of parameters associated with fixed effects.
You seek to assess the significance of a continuous-scale fixed effects factor (prop_hav) using a likelihood ratio test. The full model has 5 parameters: intercept, slope for prop_hav, and 3 variances (rep, gen, residual). The reduced model has 4 parameters: intercept, and 3 variances (rep, gen, residual). The difference in the number of parameters between the two models is 5 - 4 = 1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Compute the difference between the "-2 Log Like" of the full model and the reduced model. Then compare this statistic to the 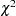 distribution with degrees of freedom equal to the difference in the number of parameters for the two models. The difference in number of estimated parameters for your example should be 1.
distribution with degrees of freedom equal to the difference in the number of parameters for the two models. The difference in number of estimated parameters for your example should be 1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks for the reply. Please have a look at the SAS script I posted. Both reduced and full model have the same number of covariance parameters which is 3.
/* reduced model*/;
proc mixed method=ml;
class rep gen;
model rtwt=/ddfm=kr;
random rep gen;
run;
quit;
/* Full model */;
proc mixed method=ml;
class rep gen;
model rtwt= prop_hav /ddfm=kr;
random rep gen;
run;
quit;
As you can see, the full model has prop_hav as a covariate. The only difference between the model is the fixed factor which is covariate. The number of parameters in each case is 3: rep variance, gen variance, and residual variance. This means the difference of -2 log likelihood with have chi-square distribution with zero degree of freedom (3-3) and NOT 1 degree of freedom.
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You misunderstand the method. Yes, the two models have the same number of parameters associated with random effects (variances or covariances), but they have different numbers of parameters associated with fixed effects.
You seek to assess the significance of a continuous-scale fixed effects factor (prop_hav) using a likelihood ratio test. The full model has 5 parameters: intercept, slope for prop_hav, and 3 variances (rep, gen, residual). The reduced model has 4 parameters: intercept, and 3 variances (rep, gen, residual). The difference in the number of parameters between the two models is 5 - 4 = 1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I'm pleased you found it helpful.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
Just posted questions on externally conditional studentized residual from proc mixed. I would appreciate your guide and assistance on this.
Thanks
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.


