- Home
- /
- Analytics
- /
- Stat Procs
- /
- How Do I Model Data That Follows an Exponential Distribution
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello,
I am looking to model data that appears to follow the exponential distribution with a mean of 1.8, as indicated by the screenshots from the CAPABILITY procedure.
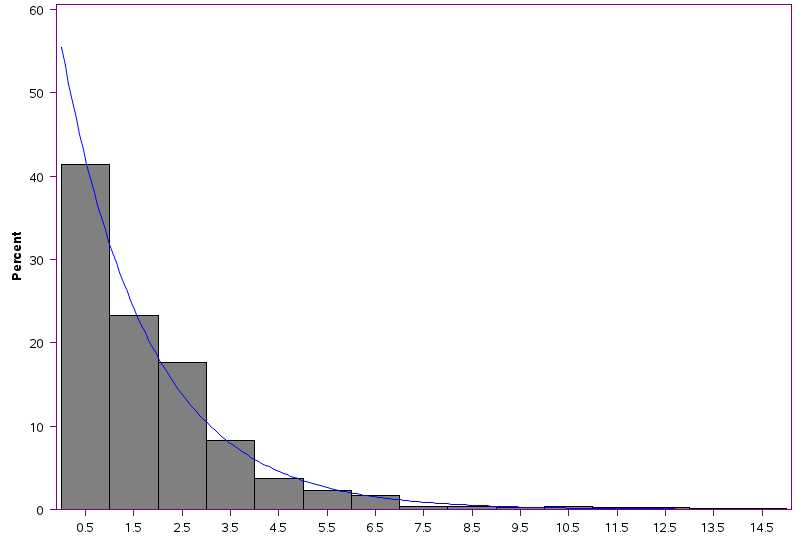
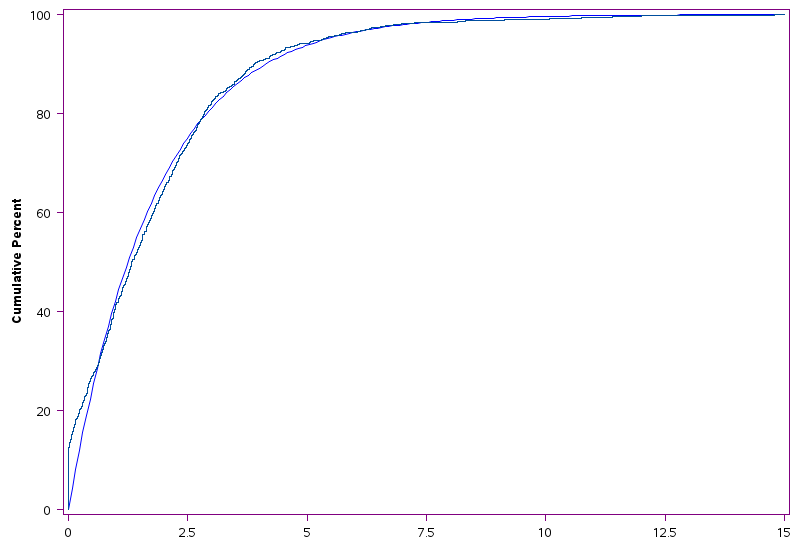
Knowing this, how would one go on about trying to build a predictive model for this data? I narrowed down the number of variables to use with the Rapid Predictive Modeler (I do not have Enterprise Miner installed on my computer) and I have tried using the MODEL procedure to do a non-linear modeling of the data but the fit is very poor with an r-square of 0.0674 and a root MSE of 1.8 (to give perspective, the mean of the data is 1.8). Any advice on this topic would be greatly appreciated!
PROC MODEL DATA=stdize_data;
PARAMETERS w_1 0
w_2 0
w_3 0
w_4 0
lambda 1;
BOUNDS w_1 >= 0,
w_2 >= 0,
w_3 >= 0,
w_4 >= 0,
lambda > 0;
RESTRICT w_1 + w_2 + w_3 + w_4 = 1;
CER = lambda * exp(-lambda * (w_1*x_1 + w_2*x_2 + w_3*x_3 + w_4*x_4));
FIT CER / MAXITER=10000 OUT=model_results OUTALL;
RUN;- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I guess I don't understand what you mean by "how do I build a predictive model." If there are no covariates, then the expected value of your model is 1.8 and the model
Y = 1.8
is the linear model that fits the data.
In your PROC MODEL statement, you have X1-X4, which appear to be explanatory variables. But if these are covariates, then you should not have used PROC CAPABILITY to fit the response, you should have used a regression procedure such as PROC GENMOD.
Please explain whether this is a univariate model or a regression problem. If regression, please describe the data.
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.


