Comparing areas under ROC curves using DeLong.

[Asockalypse]

Hi,

I am investigating various biometrics, and am comparing the results using the method of DeLong et al. and this method: http://support.sas.com/kb/25/017.html

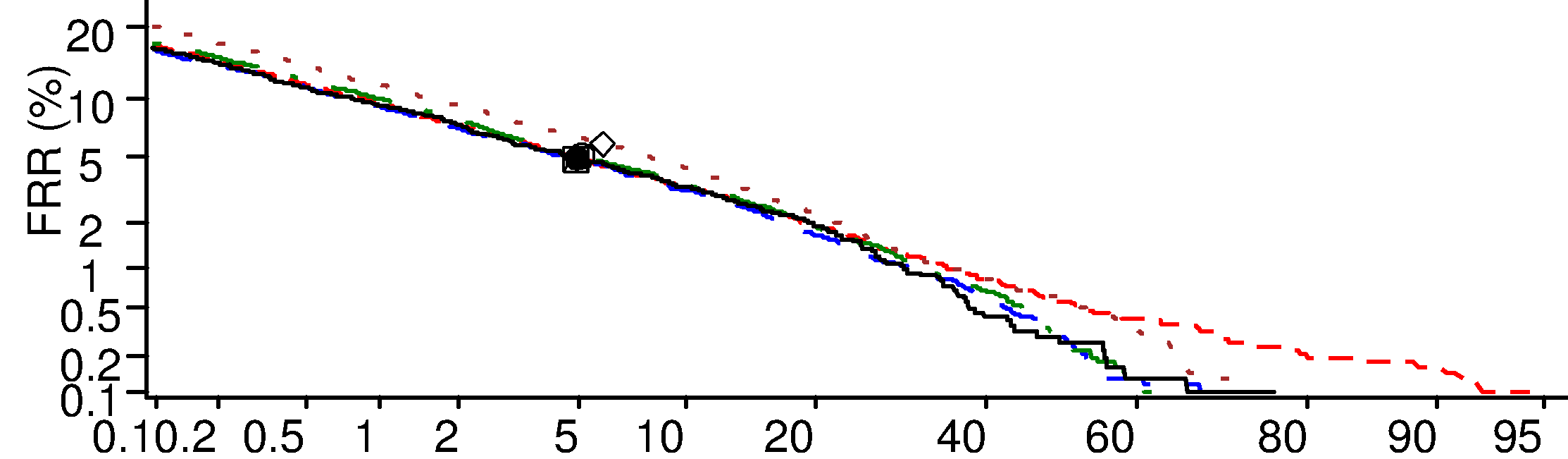
I don't have a problem with the method itself as such, and I obtain p-values indicating significantly different values in area. However after examining the ROC curves, I can see that a significant difference in area is primarily due to a significant difference between curves at high values of false accept rate as you can see in this image for the red curve compared to the black (Axes are non linear - plotted as a DET curve, false accept rate on x-axis)

As in reality a practical system would have a cut off around the equal error rate (marked on the curves) would it be valid to compare the areas between the curves just around this section, for example 0.1 to 20%, to avoid the craziness that happens at higher false accept rates? Or would that not be valid statistically?

s

As a side note, I'm not sure if the problem arises due to the number of inter and intra class comparisons I have - I only have 3,000 intra class but have 168,000 inter class. Would that explain the shape at higher false accept rates? If so is there anything I can do to alleviate it with the data I have.

Any help would be greatly appreciated!

Thanks

[Rick_SAS]

Are you comparing different models, or are these the same model, but one uses the %ROCPLOT macro whereas another uses...what? PROC LOGISTIC? Other non-SAS software?

You might want to start your comparison by using a smaller data set. The KB article that you quote has a small data set of 49 observations. For an even smaller data set, see my article on "Computing an ROC Curve from Basic Principles."  If you use one of these, it should be simple to determine whether the discrepancies that you notice are due to some fundamental difference in the algorithms or whether they are specific to your data, perhaps due to the number of inter and intra class comparisons.

Rick

[Asockalypse]

Hi, thanks for the quick reply.

In summary I am performing biometric recognition between each image with every other image to generate a set of hamming distances. These hamming distances are then used to generate the roc plot using %ROCPLOT. I am then modifying the images in some way (e.g. adding noise), generating a new set of hamming distances, and regenerating the roc plot again using %ROCPLOT. I'm then comparing the two to ascertain whether the modification affects the recognition process. As I say, I'm really interested in whether it's valid to limit the area comparison calculation into the useful area of the ROC curve.

I had a quick look before at smaller sets but I had very disjointed ROC curves rather than the comparatively smooth ones with the larger data set (as you'd expect) but I might double check how it affects them.

Cheers

[Rick_SAS]

All ROC curves are piecewise linear. They only look smooth when you have more observations.

[lvm]

I think the other issue you are getting at involves the logic of calculating the area under the entire ROC curve. Although there are some good statistical reasons to estimate this area under the entire curve (over all TPP and FPP), some authors argue against this approach. These latter authors argue for the partial area under the ROC curve (that is, the area is estimated over a narrower range of FPP, in the region where the diagnostic test is most likely to be used). A google search for "partial area under ROC curve" will give you several hits. I have not tried this with SAS -- I am guessing that one would have to write the code in IML. Pepe (an authority in this area) does have STATA code for the calculations.

[Asockalypse]

Hi Ivan, that's exactly what I was thinking about, thanks for directing me that way. I found a paper "A non-parametric method for the comparison of partial areas under ROC curves and its application to large health care data sets" that looks to be approximately the partial-area analogue to the DeLong method. Unfortunately I just don't have the skill to convert that into the required SAS/IML. Also, found the STATA code you mentioned but don't have any way of converting that to SAS.

I think without any SAS code (I'm using 9.1.3) I'm rather stumped on this line of enquiry, even though it seems like the correct one to me. If anyone is aware of code for calculating pAUC that would be great, but thanks for your help anyway.

[Rick_SAS]

You can compute a pAUC as follows:

1) Read the article "The area under an ROC Curve."

2) Following the example in the article, use the OUTROC= option to write the coordinates of the ROC curve to a SAS data set

3) Use a where clause to subset the ROC curve to the interval [a,b], where [a,b] is the region where the diagnostic test is most likely to be used.

4) The ROC curve is piecewise linear. Therefore the EXACT area can be found by using the trapezoidal rule. Write a DATA step or use the SAS/IML program in the article "The trapezoidal rule of integration" to compute the (partial) area under the curve.

Rick

[Asockalypse]

Thanks for the input Rick, I was thinking that I would be able to work it out like that and your article is a great starting point.

However I also need to determine confidence intervals and be able to compare pAUC for significant differences, I think neither of which would be possible using the method you describe.

Thanks though!