Clustering Effect Evaluation

[KyleM_Corrie]

I've been trying to come up with a method to evaluate how certain stores sales may or may not be affected once an identical store is introduced within a given proximity. With the help of some of you, I've been introduced to some pretty clever ideas to get it going.

However, in order to make this process more replicable, I think I need to be more specific. So, my end goal is to be able to evaluate average store sales for the time period each new store is introduced.

To begin:

I have a data set filled with store information (an identifier, when it opened, latitude, longitude). With a combination of macro variables, SQL, and the GEODIST function, I am able to run a program that produces which stores opened within a given year (e.g., 2006), and which stores already existed (within a selected distance) when that new store opened.

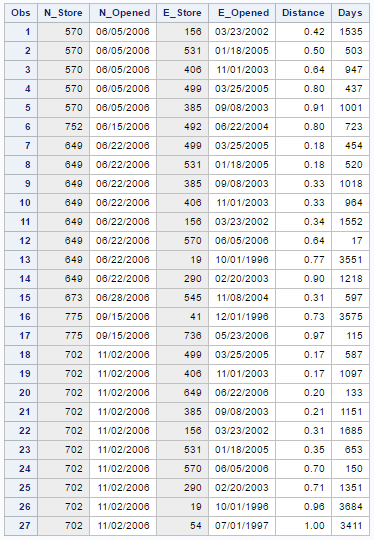
So, my results would look like the following:

Each unique value of N_Store represents a store that opened during 2006 and into a 1 mile radius of an existing store. Each value of E_Store represents those existing stores which were within a 1-mile radius of the newly opened store.

Now, this is where I'm having trouble.

I want to use this information in conjunction with a sales data set to see if, all else constant, this range affected sales of existing stores.

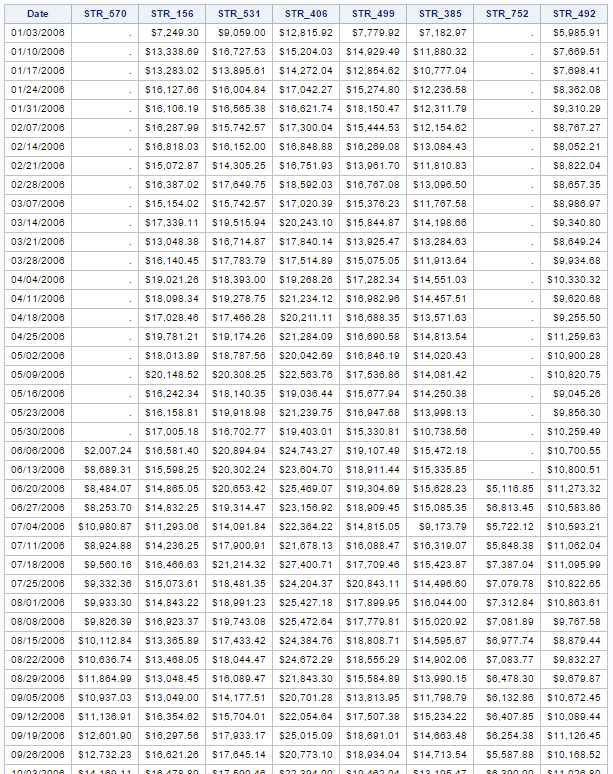
An abbreviated version of that sales data would like like the following:

So, when store 570 opened on June 6, 2006, stores 156, 531, 406, 499, and 385 already existed within a 1-mile radius. Then, later when store 752 opened on June 20, 2006, store 492 already existed within a 1-mile radius.

My goal:

I'd like to calculate the average of all stores, which already existed, for the time period before the new store was introduced. For example, for stores 156 through 385, the period would be from May 30, 2006 and before. For store 492, the period would be June 13, 2006 and before.

Then I'd also like to know what they did 1 year, 2 years, 3 years after that store was introduced. So, for stores 156 through 385, I'd be looking at a 52/104/156 week average after June 6, 2006. Then, for store 492, a 52/104/156 week average from June 20, 2006.

If anyone has any ideas on how this could be done, I'd love to hear them! If it can't be done, I'd love to hear that too!

Thanks very much.

[gergely_batho]

Hi,

Very nice problem, thank you for sharing it.

What I would do first, is to create a time-series model for each of the store sales.

The simplest time-series model would be one, that contains an explanatory variable, which is simply the count of nearby stores. This explanatory variable changes over time of course.

The parameter estimat for this variable would be the "Nearby_Store_Open" effect.

As a next model, instead of the count variable, I would use dummy variables.

For the time series of store 570 you don't need dummy variable for 156, 531, 406, 499, 385 - because they already existed, when the store was opened.

But when you analyse time series 156, you will have a EXIST_570 variable, which is 0 until 06/05/2006, and 1 after it.

To make time-series models more precise, maybe it is worth to include trend and seasonality into the model (if you have several years of data), or maybe other explanatory variables (example: store was closed for 1 day on a given week).

Sometimes events such as store_opening have a gradual effect. This means, when a nerby store opens, first it has just some minor effect on sales of the first store, the next week this effect is bigger, after some weeks this effect stabilizes. There are many way to model this.  Of course first try the simlest ideas above.

If you have SAS/ETS, I would start by looking at PROC AUTOREG (simplest), PROC ARIMA, PROC UCM (most complex)  - these are capable of using expanatory variables (regressors).

With PROC PANEL, PROC VARMAX, PROC SSM you could model all the store time-series in one model. That would be a very nice model, but I don't suggest you it right now.

If you don't have SAS/ETS, you can use SAS/STAT procedures: PROC REG, PROC GLM,...

They are not native time series models. Using them you ignore lot's of time-series specific phenomena, but still you can use them, and get good results.

If you still have time to play around, you could measure the proximity effect of other stores. The hypotheses would be: Even within 1 mile, the store distance matters.  One idea of measuring it: instead of creating 0/1 variables, you create a varaible based on the distance. The formula creating that variable... well I have think of it. Until the store does not exist, that variable shoud be 0. When the store is there, the closer it is, the higher the value. It the store is very distant, it converges to 0.

Greg