PROC EXPAND

[vickyCh]

How can I obtain the moving slope coefficients of regression analysis in a data series, like in PROC EXPAND convert /transformout=( MOVTVALUE n)  or (MOVSTD n) ? There are thousands of sales data and we want to know the sales trend.

ENTITY    DATE        sales

aaa  2003/1/2 7864500

aaa  2003/1/3 5963400

aaa  2003/1/6 7923300

aaa  2003/1/7 11907000

aaa  2003/1/8 9509700

aaa  2003/1/9 10711600

aaa  2003/1/10       9961400

aaa  2003/1/13       10499100

aaa  2003/1/14       7569200

aaa  2003/1/15       8147600

aaa  2003/1/16       10112800

aaa  2003/1/17       17332600

aaa  2003/1/21       8927000

aaa  2003/1/22       9433100

aaa  2003/1/23       8371500

aaa  2003/1/24       7748000

aaa  2003/1/27       9307800

aaa  2003/1/28       8018400

aaa  2003/1/29       7757500

aaa  2003/1/30       7349500

aaa  2003/1/31       9744100

aaa  2003/2/3    6483500

aaa  2003/2/4     9216200

aaa  2003/2/5     7427500

aaa  2003/2/6     7755200

...

[Reeza]

Is this a continuously moving slope calculation? Or a specific window?

The functions available by PROC EXPAND are here: http://support.sas.com/documentation/cdl/en/etsug/63939/HTML/default/viewer.htm#etsug_expand_sect026...

I don't think there's directly a regression slope coefficient, so my default would be to use data step functions to manually calculate the slope at each line.  

I'm also 99% sure that this has been asked and answered on here in the last 6 months. 

[vickyCh]

It is a continuously moving slope calculation.

Since there are thousands of sales data, it may not be practical to manually calculate the slope at each line if, for example, we want to know each month (30 days) sales trend (slope coefficient) difference.

[Reeza]

The number of lines wouldn’t matter to the calculation...

It’s not like you’d type out a formula for each line, just retain the components. 

How are you handling time? I’m assuming that’s the x, or do you have another variable?

---

@vickyCh wrote:

It is a continuously moving slope calculation.

Since there are thousands of sales data, it may not be practical to manually calculate the slope at each line if, for example, we want to know each month (30 days) sales trend (slope coefficient) difference.

---

[PGStats]

Maybe you could start with:

data have;
input ENTITY $    DATE :yymmdd10.  sales :12.6;
format date yymmdd10. sales best7.2;
datalines;
aaa  2003/1/2 7864500
aaa  2003/1/3 5963400
aaa  2003/1/6 7923300
aaa  2003/1/7 11907000
aaa  2003/1/8 9509700
aaa  2003/1/9 10711600
aaa  2003/1/10       9961400
aaa  2003/1/13       10499100
aaa  2003/1/14       7569200
aaa  2003/1/15       8147600
aaa  2003/1/16       10112800
aaa  2003/1/17       17332600
aaa  2003/1/21       8927000
aaa  2003/1/22       9433100
aaa  2003/1/23       8371500
aaa  2003/1/24       7748000
aaa  2003/1/27       9307800
aaa  2003/1/28       8018400
aaa  2003/1/29       7757500
aaa  2003/1/30       7349500
aaa  2003/1/31       9744100
aaa  2003/2/3    6483500
aaa  2003/2/4     9216200
aaa  2003/2/5     7427500
aaa  2003/2/6     7755200
;

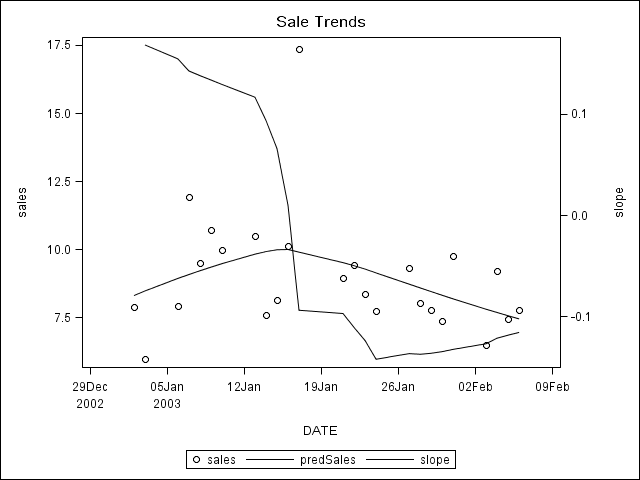
proc loess data=have plots(only)=fit;
model sales=date / direct smooth=0.8;
output out=want predicted=predSales;
run;

data wantSlope;
set want;
slope = dif(predSales) / dif(date);
run;

title "Sale Trends";
proc sgplot data=wantSlope;
scatter x=date y=sales;
series x=date y=predSales;
series x=date y=slope / y2axis;
run;

[mkeintz · Accepted solution]

PROC EXPAND can be a useful tool for rolling slopes, but you have to create cross-products (to be summed) prior to proc expand, and calculate beta afterwards.  Here's an example generating rolling 12-month slopes of closing prices in sashelp.stocks:

proc sort data=sashelp.stocks out=stocks;
  by stock date;
run;

data vneed /view=vneed;
  set stocks (keep=stock date close);
  X=intck('month','01jan1984'd,date);
  XY=X*close;
run;

proc expand data=vneed out=need2 (where=(n=12)) method=none;
  by stock;
  id date;
  convert close=n     / transformin=(*0)  transformout=(+1 movsum 12);
  convert X=sumXX     / transformout=(movuss 12);
  convert XY=sumXY    / transformout=(movsum 12);
  convert close=meanY / transformout=(movave 12);
  convert X=meanX     / transformout=(movave 12);
run;

data want;
  set need2;
  beta =   (sumXY - n*meanX*meanY) / (sumXX - n*meanX*meanX);
run;

It's relatively simple because you just want the slope.   If you define y=Y-mean(Y) and x=X-mean(X), (i.e. "de-meaned" X and Y), then the beta coefficient (slope) of Y regressed on X is the ratio of the sum(x*y)/sum(x*x). 

So no matrices needed, and the numerator and denominator above are functions of the (1) sum of products of X*Y, (2) sum of squared X, and (3) the means of X and Y.

[vickyCh]

I would like to say a big thank you to all of you for your help, especially mkeintz.
That is exactly what we want.