- Home
- /
- Programming
- /
- SAS Procedures
- /
- Re: How can I use simulation to compare Models by their probabilities?
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I was reading a paper on simulation and the author tries to compare the Poisson probabilities and the empirical (observed) probabilities for each particular covariate pattern to verify if the Poisson model fits the data accurately.
The model used in the simulations was defined by; y= 1+ x1 + 2x2 - 0x3
x1 is from a Bernoulli(0.5) distribution, x2 is from a Bernoulli(0.5) distribution, and x3 is also from a Bernoulli(0.5) distribution. Simulation results are based on 10000 replications.
My questions are;
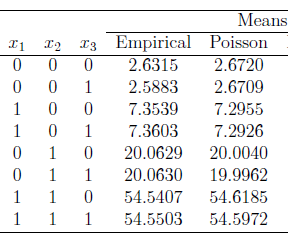
- The means from each covariate pattern from their respective distributions are shown as in the picture shown. How could I adjust my code to obtain such means? I don’t get what these means actually are. And how do I differentiate these two distributions.
%let NumSamples = 10000;
data s1;
call streaminit(1234);
do SampleID=1 to &NumSamples;
x1=rand("Bernolli",0.5);
x2=rand("Bernolli",0.5);
x3=rand("Bernolli",0.5);
mu = exp(1 + x1 + 2*x2 - 0*x3);
y = rand("poisson", mu);
output;
end;
run;2. Each covariate pattern has a different set of probabilities based on the above means. I don’t understand how I would calculate probabilities especially on empirical distribution. i.e for the pattern x1=1, x2=0, x3=0 the probability under Poisson is 0.0007 while that based on empirical distribution is 0.0032
- Tags:
- poisson
- simulation
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The point of doing a simulation is usually to compare an observed value with the distribution of simulated values. If your observed value is outside the bulk of simulated values then you can infer that it is not compatible with one or more of your simulated process assumptions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Calling @Rick_SAS
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
> I was reading a paper on simulation and the author ...
If you are going to make a reference to the literature, please provide a full reference.
It's probably fruitless to make a guess based on what you've written, but I'll try my best.
Notice that mu does not depend on the x3 variable at all when the linear combination is 1 + x1 + 2*x2 - 0*x3. However, the table that you pasted also doesn't depend on x3, so the table and the formula are consistent.
The linear combinations
lambda = 1 + x1 + 2*x2
is the base-two representation of the digits [1,4]. That expression is equivalent to
lambda = rand("Integer", 1, 8); /* SAS 9.4m5 */
or
lambda = ceil( 8*rand("uniform") );
That makes the Poisson random variable Y ~ Pois(exp(lambda)) a linear combination (mixture model) of four Poisson rv's:
Pois(exp(1)), Pois(exp(2)),..., and Pois(exp(4)). I suspect that you can analytically compute the mean of a linear combination of k Poisson rv's with equal coefficients 1/k.
I would have expected that the mean of a Pois(exp(1)) to be 2.718, whereas the table gives 2.67, so clearly I do not understand all that is going on, but maybe these thoughts will trigger some ideas of your own. Good luck.
Learn the difference between classical and Bayesian statistical approaches and see a few PROC examples to perform Bayesian analysis in this video.
Find more tutorials on the SAS Users YouTube channel.
SAS Training: Just a Click Away
Ready to level-up your skills? Choose your own adventure.