- Home
- /
- Programming
- /
- SAS Procedures
- /
- Determine top five winners in a series of races
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Glad to see you back, PGStats.
What is the significance of "not trivial to compute"? Does that mean this will work for small data sets, but not large ones? (Worked just fine, by the way -- copied and pasted directly into SAS. Same result as Reeza's way.) Seems the key improvement would be in solving the issue of ties.
By the way, if any runner misses one race does that mean he's screwed for the series?
Do you have a view on the PCA approach Ksharp mentioned?
Thanks much!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Reeza 's method take every race as a single thing separately. It don't care the relations between races . E.X. someone who wins 50-meter will be more possible winning 100-meter. Multi-variable analysis take these data as a whole data ,use one or two principle componet to present this Matrix , and take care of this relationship between races.
Ksharp
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
In my experience, the first principal component when dealing with sufficiently regular variables is often the positively weighted sum of all variables, i.e. something similar to Reeza's ranking method.
PG
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hate to keep being a bother... I've added a fifth line of data, and made two results missing. Running your script with this modified data set there appears in results nothing for runner C. Would you please check your script and change as needed? Thank you very much. Perhaps C doesn't get listed because of last place finish?
data input;
input rank (race1-race3) ($) ;
cards;
1 D E D
2 A D B
3 E . A
4 C B C
5 B C .
;
data list;
set input;
array race race:;
do _n_ = 1 to dim(race);
name = race{_n_};
output;
end;
drop race:;
run;
proc freq data=list noprint;
table name*rank / sparse out=scores(drop=percent);
run;
proc transpose data=scores out=scoreTable(drop=_:) prefix=r_;
var count;
by name;
id rank;
run;
proc sort data=scoreTable; key r_: / descending; run;
proc print data=scoreTable(obs=5) obs="Final rank"; run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Your original request did not involve missing names. You may allow for the possibility of missing names in your table by replacing statement output; in the dataset list creation step by if not missing(name) then output;
you will get the expected overall ranking:
Final
rank name r_1 r_2 r_3 r_4 r_5
1 D 2 1 0 0 0
2 E 1 0 1 0 0
3 A 0 1 1 0 0
4 B 0 1 0 1 1
5 C 0 0 0 2 1
PG
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Beautiful. Works like a charm.
Now three alternatives in hand to determine race outcome, all three yielding the same results, but apparently going about it slightly differently.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Here is the contribution provided by given on another thread. This translates the Basketball example which uses PCA earlier mentioned by :
data input;
input rank (race1-race3) ($) ;
cards;
1 D E D
2 A D B
3 E . A
4 C B C
5 B C .
;
run;
data _null_;
if _n_ eq 1 then do;
length order1 - order3 8 k $ 8;
declare hash ha(ordered:'y');
ha.definekey('k');
ha.definedata('k','order1','order2','order3');
ha.definedone();
end;
set input end=last;
array o{3} order1-order3 ;
array r{3} race1-race3 ;
do i=1 to dim(r);
if not missing(r{i}) then do;
k=r{i};
rc=ha.find();
o{i}=rank;
ha.replace();
call missing(of order:);
end;
end;
if last then ha.output(dataset:'bballm');
run;
proc means data=bballm noprint;
output out=maxrank
max=morder1 morder2 morder3 ;
run;
data bball;
set bballm;
if _n_=1 then set maxrank;
array services[3] order1-order3;
array maxranks[3] morder1-morder3 ;
keep k order1-order3 ;
do i=1 to 3 ;
if services=. then services=maxranks+1;
end;
run;
ods graphics on;
proc prinqual data=bball out=tbball scores n=1 tstandard=z
plots=transformations;
transform untie(order1-order3);
id k ;
run;
* Perform the Final Principal Component Analysis;
proc factor nfactors=1 plots=scree;
ods select factorpattern screeplot;
var Torder1-Torder3 ;
run;
proc sort;
by Prin1;
run;
* Display Scores on the First Principal Component;
proc print;
var k Prin1;
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
As being hinted by above multiple answers, especially the one from PG's vs. others, at current stage, your problem is more of the methodology question than a SAS one. For example, there are many different ranking (rating) system in the world of sport. In the real world, Racers are ranked by their absolute scores (Usain Bolt: 9.58 sec) instead of relative ones, which makes more sense if the measurements are controlled well. Giving the relative scores you have, you are looking at something similar to the ranking systems such as Tennis or Golf. Again, in the real world, the weight of scores barely spreads evenly (eg. PG suggested), take Golf for example, in a major tournament, if the Champion gets 1000, the quarter-final only gets 250. That being said, it is your call to come up whatever ranking system you think is reasonable for your problem, and SAS will surely take care of the rest mechanical part of job.
Haikuo
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Note that you can get a large family of rankings in the following way. If you define
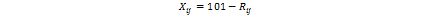
where Rij is the rank of runner i in race j and a monotone increasing function f then

will be a valid ranking. Expressed that way, Reeza's method is based on
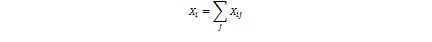
and mine on
PG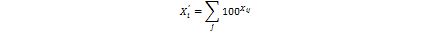
- « Previous
-
- 1
- 2
- Next »
SAS Innovate 2025: Save the Date
SAS Innovate 2025 is scheduled for May 6-9 in Orlando, FL. Sign up to be first to learn about the agenda and registration!
Learn the difference between classical and Bayesian statistical approaches and see a few PROC examples to perform Bayesian analysis in this video.
Find more tutorials on the SAS Users YouTube channel.
SAS Training: Just a Click Away
Ready to level-up your skills? Choose your own adventure.




