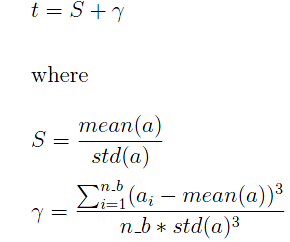- Home
- /
- Programming
- /
- SAS Procedures
- /
- Re: Calculating expression of a formula for each resample
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I have a datafile called 'original' and in it contains 4 variables, call them a, b, c, d, with n observations each. I then use proc surveyselect to draw 1000 resamples from the 'original' dataset with sample size n_b = n/4, the code is as follows:
proc sql noprint;
select ceil(count(*)/4) into :record_count
from original;
quit;
%put &record_count;
%let rep = 1000;
proc surveyselect data= original out=bootsample
seed = 1234 method = urs
sampsize=&record_count outhits rep = &rep;
run;
ods listing close;
This produces a datafile named 'bootsample' which contains 1000 samples with sample size n_b of each variable (a, b, c, and d) from the 'original' dataset. Each observation's replication ID is given by the variable "Replicate" (ranging from 1 to 1000).
What I need to do is this:Take Replicate = 1 (i.e., the first replication sample) and the variable a as an example. I want to calculate the following value of t: (if the picture below doesn't show, please see attachment of the picture titled "formula")
where mean(a) is the sample average of the variable a for replication sample 1, std(a) is the sample standard deviation of the variable a for replication sample 1, a_i represents each individual observation of the variable a for replication sample 1.
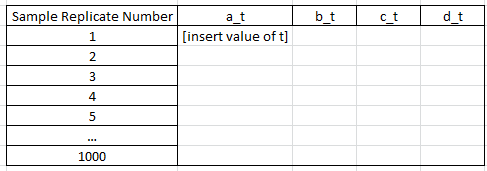
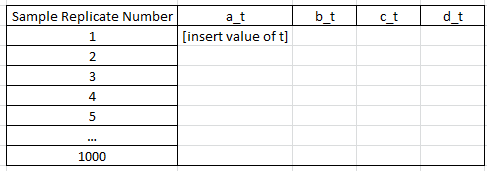
Then, I want to repeat the above procedure and calculate the value of t for all 1000 replication samples and all four variables: a, b, c, and d. I want to store the final result in a datafile called "result" that has 4 variables called a_t, b_t, c_t, and d_t (i.e., 4 columns) and the 1000 values of t of each variable in each row. So, graphically, a datafile structured like this: (if the picture below doesn't show, please see attachment of the picture titled "result")
Can anyone show me a template code that can achieve what I described above? I'm thinking maybe proc sql can do the trick, but I'm quite new to SAS and still don't really know the syntax very well. Thanks.
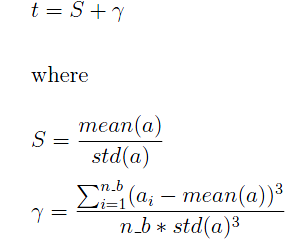
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Sure, PROC SQL can do the trick, but PROC MEANS (or PROC SUMMARY for that matter) can compute more statistics than PROC SQL, e.g. skewness (thanks, @Reeza, for the hint!). Please note that your S statistic can be derived from the coefficient of variation: S=100/CV. Your g statistic can be calculated directly as skewness with the VARDEF=N option of the PROC MEANS statement, whereas your sample standard deviation would require VARDEF=DF (for the denominator n-1, which I assume is what you want). Instead of merging two datasets with summary statistics (one for each setting of VARDEF), I decided to convert the default "DF skewness" to "N skewness" by multiplying with the appropriate conversion factor f := (n-1)(n-2)/n² = 1 - 3/n + 2/n².
proc summary data=bootsample;
by replicate;
var a b c d;
output out=stats(drop=_:) cv= skew= / autoname;
run;
%let f=%sysevalf(1-3/&record_count+2/&record_count**2);
data want;
set stats;
a_t=100/a_CV+&f*a_Skew;
b_t=100/b_CV+&f*b_Skew;
c_t=100/c_CV+&f*c_Skew;
d_t=100/d_CV+&f*d_Skew;
drop a_CV--d_Skew;
run;
ods html file="C:\Temp\t_stat.html";
ods listing close;
title 'The t Statistic';
proc print data=want label noobs;
run;
ods html close;
ods listing;
title;
This could be the PROC SQL code (perhaps for validation purposes or for comparison of run times and numerical accuracy):
proc sql;
create table want as
select replicate,
m_a/s_a+sum(x_a)/(&record_count*s_a**3) as a_t,
m_b/s_b+sum(x_b)/(&record_count*s_b**3) as b_t,
m_c/s_c+sum(x_c)/(&record_count*s_c**3) as c_t,
m_d/s_d+sum(x_d)/(&record_count*s_d**3) as d_t from
(select replicate, mean(a) as m_a, std(a) as s_a, (a-calculated m_a)**3 as x_a,
mean(b) as m_b, std(b) as s_b, (b-calculated m_b)**3 as x_b,
mean(c) as m_c, std(c) as s_c, (c-calculated m_c)**3 as x_c,
mean(d) as m_d, std(d) as s_d, (d-calculated m_d)**3 as x_d
from bootsample
group by replicate)
group by replicate;
quit;Minor differences (like 1E-13, but depending on your a, b, c, d values) between the two approaches are likely to occur.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Here's some sample code.
Proc means data=have stackods n mean median std max min;
By replicate;
Var a b c d t;
Ods table summary=Results;
Run;
Proc print data=results;
Run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Basically, the trouble I am having is how to code the formula and also how to output the results.
Thanks for your help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Sure, PROC SQL can do the trick, but PROC MEANS (or PROC SUMMARY for that matter) can compute more statistics than PROC SQL, e.g. skewness (thanks, @Reeza, for the hint!). Please note that your S statistic can be derived from the coefficient of variation: S=100/CV. Your g statistic can be calculated directly as skewness with the VARDEF=N option of the PROC MEANS statement, whereas your sample standard deviation would require VARDEF=DF (for the denominator n-1, which I assume is what you want). Instead of merging two datasets with summary statistics (one for each setting of VARDEF), I decided to convert the default "DF skewness" to "N skewness" by multiplying with the appropriate conversion factor f := (n-1)(n-2)/n² = 1 - 3/n + 2/n².
proc summary data=bootsample;
by replicate;
var a b c d;
output out=stats(drop=_:) cv= skew= / autoname;
run;
%let f=%sysevalf(1-3/&record_count+2/&record_count**2);
data want;
set stats;
a_t=100/a_CV+&f*a_Skew;
b_t=100/b_CV+&f*b_Skew;
c_t=100/c_CV+&f*c_Skew;
d_t=100/d_CV+&f*d_Skew;
drop a_CV--d_Skew;
run;
ods html file="C:\Temp\t_stat.html";
ods listing close;
title 'The t Statistic';
proc print data=want label noobs;
run;
ods html close;
ods listing;
title;
This could be the PROC SQL code (perhaps for validation purposes or for comparison of run times and numerical accuracy):
proc sql;
create table want as
select replicate,
m_a/s_a+sum(x_a)/(&record_count*s_a**3) as a_t,
m_b/s_b+sum(x_b)/(&record_count*s_b**3) as b_t,
m_c/s_c+sum(x_c)/(&record_count*s_c**3) as c_t,
m_d/s_d+sum(x_d)/(&record_count*s_d**3) as d_t from
(select replicate, mean(a) as m_a, std(a) as s_a, (a-calculated m_a)**3 as x_a,
mean(b) as m_b, std(b) as s_b, (b-calculated m_b)**3 as x_b,
mean(c) as m_c, std(c) as s_c, (c-calculated m_c)**3 as x_c,
mean(d) as m_d, std(d) as s_d, (d-calculated m_d)**3 as x_d
from bootsample
group by replicate)
group by replicate;
quit;Minor differences (like 1E-13, but depending on your a, b, c, d values) between the two approaches are likely to occur.
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
Learn the difference between classical and Bayesian statistical approaches and see a few PROC examples to perform Bayesian analysis in this video.
Find more tutorials on the SAS Users YouTube channel.
SAS Training: Just a Click Away
Ready to level-up your skills? Choose your own adventure.