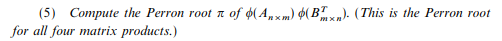Proc IML Matrix products incorrect?

[cwigtil]

I am working with a 3000 x 55 matrix with cell values of either 0 or 1, which I am transposing & mirroring the contents (0 becomes 1 & vice versa), then multiplying to obtain four product matrices. Mathematically, this procedure should yield a single Perron root across all 4 product matrices, but I am not obtaining this result. I double-checked my code for accuracy.

I’m wondering if Proc IML with the EIGEN call has difficulty with calculating eigenvalues for such large matrices? The eigenvalues seem accurate because the largest ones for the 3000 x 3000 product matrices match those of the 55 x 55 matrices.

[Rick_SAS]

Could you provide an example of your computations? Since eigenvalues only apply to square matrices, I am not sure what you are doing with the (x x p) matrix. It sounds like you are comparing eigenvalues of X`X and XX`, but I don't understand what the other two matrices are. For example, here is one possible computation. Am I close?

proc iml;
X = {1 0,
     0 1,
     1 0,
     0 1};
notX = ^X;
A1 = X`*X;
A2 = X*X`;
A3 = notX`*notX;
A4 = notX*notX`;

v1 = eigval(A1);
v2 = eigval(A2);
v3 = eigval(A3);
v4 = eigval(A4);
print v1 v3, v2 v4;

Also, please specify which version of SAS you are running:

%put &SYSVLONG4;

[cwigtil]

Thank you so much for your reply.

Data are known and verified to only have values of 0 or 1 and to not have missing values, the original matrix (A) is "mirrored" (A') as its complement as follows:

do i=1 to 55;
  vara_p(i) = abs(vara(i)-1);
end;

Both original & complement are then transposed (B & B') & multiplied as A*B', A'*B, B*A', B'*A; regarding computation:

proc iml;
use a_orig;
read all var _num_ into y;
use b_transp;
read all var _num_ into i;
c = y * i;

create Out var {c};
append;
close Out;
quit;

Similarly I made an i*y for the same two matrices, then calculated products for the other two matrices.

The output for the four product matrices were two 3,025-long & two 9,709,456-long outputs, each of which I recognized as the square of 55 & 3116, the dimensions of the respective product matrix, so I reconfigured each of those to create the square matrices via datasteps. I then made a dataset (e.g., c_prod) for the square product matrices:

proc iml;
use c_prod;
read all var _num_ into C;
call eigen(val, rvec, C);
print val;
quit;

There should be a single Perron root across all four square product matrices, but unfortunately, that's not what I'm finding:

http://www.psych.purdue.edu/~ehtibar/publications/DSDS.pdf :

SAS version: 9.04.01M5P09132017

Take care,

~Cliff

[PaigeMiller]

---

@cwigtil wrote:

I’m wondering if Proc IML with the EIGEN call has difficulty with calculating eigenvalues for such large matrices? The eigenvalues seem accurate because the largest ones for the 3000 x 3000 product matrices match those of the 55 x 55 matrices.

---

It is my understanding that the eigenvalues of x' * x should be equal to the eigenvalues of x * x'.

[Rick_SAS]

The nonzero eigenvalues are the same, yes. But the 3000 x 3000 matrix is highly degenerate since it has at least (3000-55) zero eigenvalues.

[PaigeMiller]

---

@Rick_SAS wrote:

The nonzero eigenvalues are the same, yes.

---

That's what I meant

[Rick_SAS]

Thank you for posting more information. It would be helpful if you could modify the following example to show what computations you are doing after you get the eigenvalues. How are you comparing the eigenvalues? What computations are you doing to determine if they are equal?

proc iml;
A = {1 0 1,
     0 1 1,
     1 0 1,
     0 1 1,
     1 1 1,
     1 1 0,
     0 0 0};
B = ^A;

C1 = A*B`;
C2 = B*A`;   /* C2 = C1` so they have the same eigenvalues */
C3 = A`*B;
C4 = B`*A;   /* C4 = C3` so they have the same eigenvalues */

v1 = eigval(C1);
v2 = eigval(C2);
v3 = eigval(C3);
v4 = eigval(C4);
print v1 v2, v3 v4;

A few observations that might help:

1. C1 and C2 should have the same eigenvalues. Similarly, C3 ad C4 should have the same eigenvalues. However, these matrices do not have to be symmetric. For an unsymmetric matrix, the eigenvalues do not have to be real. Therefore, they are returned as a k x 2 matrix, where the first column contains the real part and the second contains the imaginary part (possibly 0) for each eigenvalue.

2. Even though the matrices have the same theoretical eigenvalues, the C1 and C2 matrices will contain thousands of zero eigenvalues. A system that has many repeated eigenvalues is highly degenerate. Even in the best situation, the "zero eigenvalues" will likely be small values such as 1.234e-14. When you compare eigenvalues, make sure you do not compare these finite-precision results with 0 by using an exact comparison.

I look forward to seeing how you are comparing the eigenvalues.

[cwigtil]

Thanks so much for your reply.

Actually, I'm only checking that the largest real number eigenvalue of each product is the same (which is the Perron root), because this is what Double Skew-Dual Scaling should yield across all four product matrices. Because SAS lists these in descending order by default, I only need to check the largest real number eigenvalue at the top (unless I'm wrong?). 

Thinking about this problem, I may need to drop a variable which has only values of 1; I think this might create problems in the product matrices.

[Rick_SAS · Accepted solution]

It shouldn't matter if you have a constant column.

[cwigtil]

I re-did the code and got a consistent Perron root: hooray!