Operations Research with IML, Example Quadratic Programming

[acordes]

In my autodidactic approach towards knowledge in SAS IML I read the interesting article: 

Example 9.10 Quadratic Programming :: SAS/IML(R) 13.2 User's Guide

This prompted me to apply this technique to a  different problem exposed in the recommendable book

"Schaum's Outline of Operations Research".

In doing so I cash in on the following advantages: to reassure myself of the correctness of the solution I get by solving it with IML and secondly being guided with te recipe to state the problem and define the objective function and the restrictions.

And it works! although I must confess that my higher mathematics university course lays far in the past and I don't succeed in understanding completely what's the reasoning with the eigenvalue...

If someone wants to explain me that, I'm willing to put an effort in understanding it

And generally speaking about Operations Research in IML, can someone give me advice on how to define a Travelling Salesman Problem via IML (not OR) which is additionally subject to some restrictions? I manage to formulate most of the restrictions but I fail to force the solution to being a round trip (once arriving at node B continue travelling from there ...).   

Here comes the case description as an excerpt from the mentioned book.

 

proc iml;
start qp( names, c, H, G, rel, b, activity);
   if min(eigval(h))<0 then do;
      error={'The minimum eigenvalue of the H matrix is negative.',
             'Thus it is not positive semidefinite.',
             'QP is terminating.'};
      print error;
      stop;
   end;
   nr=nrow(G);
   nc=ncol(G);

   /* Put in canonical form */
   rev = (rel='<=');
   adj = (-1 * rev) + ^rev;
   g = adj# G;
   b = adj # b;
   eq = ( rel = '='  );
   if max(eq)=1 then do;
      g = g // -(diag(eq)*G)[loc(eq),];
      b = b // -(diag(eq)*b)[loc(eq)];
   end;
   m = (h || -g`) // (g || j(nrow(g),nrow(g),0));
   q = c // -b;

   /* Solve the problem */
   call lcp(rc,w,z,M,q);

   /* Report the solution */
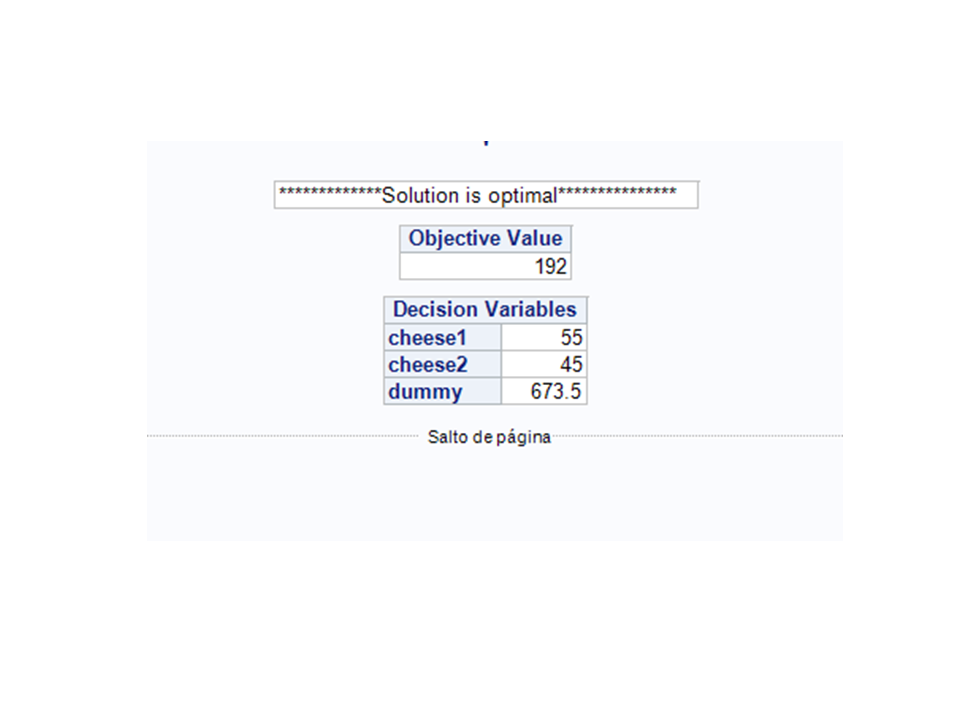
   print ({'*************Solution is optimal***************',
           '*********No solution possible******************',
           ' ', ' ', ' ',
           '**********Solution is numerically unstable*****',
           '***********Not enough memory*******************',
           '**********Number of iterations exceeded********'}[rc+1]);
   activity = z[1:nc];
   objval = c`*activity + activity`*H*activity/2;
   print objval[L='Objective Value'],
         activity[r=names L= 'Decision Variables'];
finish qp;


c = { -7.6, -5, 1};
h = { 0.08 0 0 ,
		0 0.04 0,
		0 0 0};
g = {  0.2 0.2 0 ,
      0.8 0.3 0,
	  1 0 0,
	  0 1 0,
	0 0 1};

/* constraints: */
b = { 20 , 60, 30, 30, 673.5 };
rel = { '<=', '<=', '>', '>', '=' };
names = 'cheese1':'cheese3';
names [3]= 'dummy';
run qp(names, c, h, g, rel, b, activity);

[Rick_SAS]

There is a class of matrices with nice properties that called positive definite (PD) matrices. One of their defining properties is that all eigenvalues are positive.

In a QP problem, if the H matrix is PD then the objective function is "bowl shaped." That means that there is a unique solution to the unconstrained problem and a solution exists for a properly formed constrained problem.  

If the H matrix is not PD, it might be that the graph of the objective function is an "upside down" bowl, which has no minimum. Or the graph of the objective function might be a saddle-shaped surface, which also has no minimum. In either case, the program aborts the computation because there is no global minimum, although there will be a local minimum if the constrained region is finite in extent.

[acordes]

Many thanks Rick for this excellent explication.
Your examples, posts and answers make me want to learn more and more IML.
It's fantastic and its usage seems unconstrained ☺

[Ksharp · Accepted solution]

"can someone give me advice on how to define a Travelling Salesman Problem via IML (not OR) "
Check Genetic Algorithm in IML documentation. There is already an example to solve it .
If you want use IML to solve OR problem, then you have to know GA. GA could be applied to any kind of OR problem and large scale OR problem,but it can't guarantee to get the solution.

[Rick_SAS]

And for quadratic programs, you don't need to extend the system and use LP. You can use the NLPQUA subroutine to directly solve the quadratic program in a natural way. See "Quadratic optimization in SAS."