- Home
- /
- Analytics
- /
- Forecasting
- /
- Re: ARIMA model to proc ARIMA
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi,
I am working on an intervention/ITS analysis. I first ran the analysis in R and would like to marginally replicate my results in SAS but I am having trouble. Given my ARIMA model from R and current proc arima code, I was hoping that you could point me in the right direction as the results do not make sense.
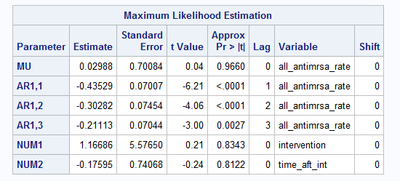
R model ARIMA=(3,0,0)
proc arima data=one;
identify=y cross=(step ramp);
estimate p=3 input=(step ramp) method=ml outmodel=out;
run;
results
SAS
R
Thank you!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
hello @Levi_M
I do not have knowledge about R code or output to know exactly the equation that is being fit in your R code to compare with your PROC ARIMA code. So I can only comment on what your PROC ARIMA code is doing, it is an ARIMA(3,0,0) model with two input series (which is a regression with AR(3) error). The model is estimated using maximum likelihood estimation method in your code with method = ML option. The mathematical equation for the ARIMA(3,0,0) model with two input series in your PROC ARIMA is below:
Y_t = mu + w1*X1_t + w2*X2_t + 1/ (1-phi1*B-phi2*B^2-phi3*B^3) *a_t
You may also check the following section of PROC ARIMA documentation for discussions of regression with ARMA errors, and the mathematical equation specified, for similar regression models with ARMA errors in general:
The example in the doc above is ARIMA(1,0,1) with two inputs, different than the one you specified, but it should give you an example what equation is being fit when regression with ARMA error is fit in PROC ARIMA in general.
You may want to verify the equation being fit in your R code and make sure the equation fit are the same before you make any comparison.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
hello @Levi_M
I do not have knowledge about R code or output to know exactly the equation that is being fit in your R code to compare with your PROC ARIMA code. So I can only comment on what your PROC ARIMA code is doing, it is an ARIMA(3,0,0) model with two input series (which is a regression with AR(3) error). The model is estimated using maximum likelihood estimation method in your code with method = ML option. The mathematical equation for the ARIMA(3,0,0) model with two input series in your PROC ARIMA is below:
Y_t = mu + w1*X1_t + w2*X2_t + 1/ (1-phi1*B-phi2*B^2-phi3*B^3) *a_t
You may also check the following section of PROC ARIMA documentation for discussions of regression with ARMA errors, and the mathematical equation specified, for similar regression models with ARMA errors in general:
The example in the doc above is ARIMA(1,0,1) with two inputs, different than the one you specified, but it should give you an example what equation is being fit when regression with ARMA error is fit in PROC ARIMA in general.
You may want to verify the equation being fit in your R code and make sure the equation fit are the same before you make any comparison.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thank you for your feedback. Unfortunately, I do not know R very well either and a package was using fit parameters ie AIC to determine the model without providing much context. However, the resources you provide helped me continue working on my project.
Thank you.
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
- Ask the Expert: Wie kann ich Visual Studio Code als SAS Entwicklungsumgebung nutzen? | 11-Dec-2025
- Ask the Expert: Marketing Decisions Excellence: Turning Insights Into Business Impact | 16-Dec-2025
- SAS Bowl LVII, SAS Data Maker and Synthetic Data | 17-Dec-2025
- DCSUG presents SAS OnDemand for Academics: the Easy Way to Learn SAS For Free for Students, Educator | 27-Jan-2026
- SAS Innovate 2026 | Grapevine, Texas | 27-Apr-2026