- Home
- /
- Analytics
- /
- SAS Data Science
- /
- Re: Oversampling and Decision tree help Plz!
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
hello everyone,
I am using SAS Enterprise Miner to create a model for a categorical response variable (0,1)..
since my event rate is about 2% and non-event rate is 98%, I have oversampled so that I have the following Proportions 30% event, 70% nonevent rate.
these are the Results from Oversampling
Data=TRAIN
Variable Value Count Percent
Resp 0 3035 70%
Resp 1 1301 30%
At this point I correct for the bias in the sample by adding a decision node to adjust the priors right before placing a decision tree node. here is the flow process.
my question is as follows: since after the oversampling, the number event instances is 1301 why do I get only 86.72 event instances in the root node:
just to be clear : when I have oversampled I got 1301 for event and 3035 non-event. when I add decision node I get 86.75 event and 4249 non-event. why is that?
Thank you in advance
your help is greatly appreciated
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi.
No, SAS EM does not think you only have 86.72 events. The display is adjusting the counts to reflect the adjusted priors. There might be a display setting that turns the adjustment off (I don't know). In any case, the computational code knows about all the observations.
The adjustments can change the computations in three places: 1. Depending on user-properties, the split search will act as if there are 86.72 events or as if there are 1301 events. 2. Depending on user-properties, the tree can be retrospectively pruned based on the adjusted numbers or the unadjusted numbers. 3. The posterior probabilities will be adjusted. I am guessing that the default behaviour for 1 and 2 is to not incorporate the adjustments. Why: because typically the adjustment makes the event look more rare, and rare events typically fool trees into being too small.
As you point out, the data step code coming out of logistic includes code at the end to adjust the posterior probabilities. The decision tree code does not output corresponding code because it outputs posterior probabilities that are already adjusted: decision tree computes the adjustments before outputing the data step code.
Let us know if you still have questions.
-Padraic
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
What is the purpose of adding the Decision Node after you already oversampled it? could you share details inside the Decision Node? Apparently it flips back to pre-oversample ratio. Hope this helps. Jason Xin
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
hi,
thank you for responding,
shouldnt I add a decision node after I oversample? or should I add it before hand? this is how I corrected for the oversampling in the decision node:
if you could tell me what am I doing wrong ( is my flow process wrong)?, I would really apreaciate it. I am really stuck here.
Thanks for you help
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello,
thank you responding!
If I understand you correctly, I will need to place decision code before oversampling. right?
thank you
Thanks
nabil
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
would this flow process be more appropriate and will it adjust my posterior probabilities?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
would this flow process be more appropriate and will it adjust my posterior probabilities?
Thanks again, you have been awesome!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Data partition Node is different: you are creating training, validation, testing. If this is your goal, it then stays in the flow. Hope this helps. Jason Xin
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi Jason,
thank you for responding
I dont think I was clear from the begining. let me walk you through the steps I have taken.
I have an origninal dataset that I oversampled ,patitioned, placed a decisions node to adjust my posterior probabilities and lastly I used the decision tree to model it, (I have taken all these steps in SAS Enterprise Miner only, I havent used base sas) here is the view:
Now in the original dataset the event rate is 2% and the non-event rate is 98%, when I oversample the event rate becomes 30% and the non-event rate is 70% .
In data partion node my training dataset contains : 3035 non-event rate and 1301 event rate for a total of 4336 observations
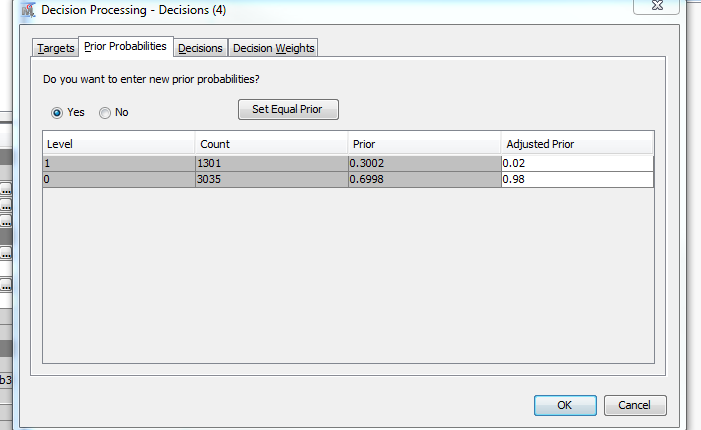
In the decion node: I adjust the priors to 2% event and 98% non-event as shown below:
Now, onto the decision tree:
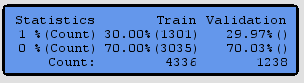
if I dont use the decision node to adjust the priors , I get these proportions (30% event, 70% non-event)
and counts (1301 events ,3035 non-event)at the root node:
which is correct given I didnt adjust for priors.
Now when I use the decision node to adjust the priors, I get these proportions (2% event,98%non-event)
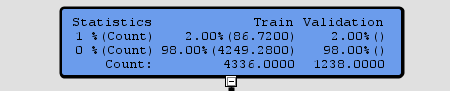
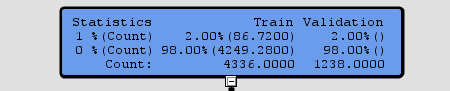
and counts (86.72 event,4249 non-event) at the root node:
what I am trying to understand is that does sas enterprise miner think that I have only 86.72 events instead of 1301 or what is going on here? ( I am really confused about this) (I know the total number of observation is correct =4336)
Also when I build a logistic regression on the same oversampled dataset , I open the results and under view ->SAS Code , I get the updated probabilities as such:
*** Update Posterior Probabilities;
_P0 = _P0 * 0.02 / 0.2997;
_P1 = _P1 * 0.98 / 0.7003;
drop _sum; _sum = _P0 + _P1 ;
if _sum > 4.135903E-25 then do;
_P0 = _P0 / _sum;
_P1 = _P1 / _sum;
end;
that's how I know that sas adjusted my posterior probabilities ,on the other hand when using decion trees, I dont get this code.
I hope I explained myself better this time.
Thanks you Jason so much for your help
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi.
No, SAS EM does not think you only have 86.72 events. The display is adjusting the counts to reflect the adjusted priors. There might be a display setting that turns the adjustment off (I don't know). In any case, the computational code knows about all the observations.
The adjustments can change the computations in three places: 1. Depending on user-properties, the split search will act as if there are 86.72 events or as if there are 1301 events. 2. Depending on user-properties, the tree can be retrospectively pruned based on the adjusted numbers or the unadjusted numbers. 3. The posterior probabilities will be adjusted. I am guessing that the default behaviour for 1 and 2 is to not incorporate the adjustments. Why: because typically the adjustment makes the event look more rare, and rare events typically fool trees into being too small.
As you point out, the data step code coming out of logistic includes code at the end to adjust the posterior probabilities. The decision tree code does not output corresponding code because it outputs posterior probabilities that are already adjusted: decision tree computes the adjustments before outputing the data step code.
Let us know if you still have questions.
-Padraic
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
do Decision trees compute the adjusted posteriors the same as logistic regression?
Thanks again!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Yes.
P(class j) = scale * unadjusted_P( j) * prior(j) / proportion_in_data(j),
where the scale is chosen to get sum over j of P(j) = 1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thank you very much for your help, I really appreciate that!
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
Use this tutorial as a handy guide to weigh the pros and cons of these commonly used machine learning algorithms.
Find more tutorials on the SAS Users YouTube channel.