Using SAS Viya to Select the British & Irish Lions Rugby Team: Part 3
The Method
In order to select the player options I firstly had to read in the stats for the three leagues plus player bios. A lot of this data was messy and needed wrangling into a suitable format. This was all done in base SAS code.
There are differences in the metrics for the premiership and Pro14 (United Rugby Championship) and since current season performance was important what I did was derive a single performance metric based on league performance – this then had a high weighting in the preference weightings. This performance metric was the sum of the inverse rank for players ranking in the top 10 across each category. Only variables that were equivalent across datasets were used so that players were not unfairly penalised for being in another league. Taking a sum of inverse rankings worked well here because each individual position shares similar qualities so players in positions which generally have less attacking responsibilities were not unfairly dismissed.
Figure 13 - Snippet of Pro14 League Stats
Figure 14 - Snippet of Premiership Stats
For the Six Nations data there were three years worth of player stats. However, not every player played in all three. I had considered using a weighting to lower the importance of past season performance. A good example of why this might be important is looking at Elliot Daly’s stats, he was consistently a key player for England but has moved around wing, center and fullback a lot and had a reasonably poor season following England’s loss in the world cup final. It might be misleading to incorporate his past stats as they would likely increase his chances of selection versus just his current season.
Figure 15 - Snippet of Six Nations Stats
Looking at the tournament appearance frequencies in Figure 13 we can see that 80% of players who had player in the Six Nations had appeared in all three tournaments. In this instance it made sense to take just the mean performance across all three years, however with more time it would be an obvious area of improvement to the model.
Figure 16 - Six Nations Tournament Appearance Frequencies
The model also needed a reference table for player options. This was fed in as a matrix of position coverage and coerced to a long format table. Because the datasets were web sources a lot of data had to be coerced to measure, and there were even some unbreakable space characters included which needed to be cleansed.
Figure 17 - Player Position Options Matrix
Finally, the output tables of the data prep and data wrangling were merged into a single input table for the selection model.
The final list of model inputs was:
|
Minutes Played |
|
Tries |
|
Try Assists |
|
Conversions |
|
Penalty Goals |
|
Drop Goals |
|
Metres Made |
|
Carries |
|
Metres Kicked |
|
Ball Played By Hand |
|
Passes Made |
|
Offloads |
|
Broken Tackles |
|
Knock Ons |
|
Tackles Made |
|
Missed Tackles |
|
Dominant Tackles |
|
Turnovers Won |
|
Turnovers Won In The Tackle |
|
Turnovers Conceded |
|
Handling Errors |
|
Pens Conceded |
|
Offside Penalties |
|
Scrum Penalties |
|
Lineouts Won |
|
Lineouts Stolen |
|
Yellow Cards |
|
Red Card |
|
Lion_Caps |
|
Nation_Caps |
|
Premier_Club_Caps |
|
age_absdev |
|
caps_age_ratio |
|
league_perf |
|
Number of Positions Covered |
Figure 18 - Model Input Variables
Where age_absdev, caps_age_ratio and league_perf were derived metrics for absolute deviation from mean age, ratio of player caps to age and overall league performance, respectively.
The PROMETHEE algorithm macro I wrote takes three inputs: the source data to be ranked, variable weight preferences, and variable preference objective functions.
Figure 19 shows a few rows of the input dataset, note the macro performs the data standardisation step so we can enter raw data. The model performs selections on 30 inputs
Figure 19 - Snippet of Model Input Dataset
In Figure 20 you can see the preference weight matrix. This is in a matrix format because each position has different qualities we want to select from. An obvious example is that positions 1-8 have no kicking responsibilities (though Johnny Hill hasn’t quite got that message this season), we can see that the preference weights for Conversions, Penalty Goals and Drop Kicks has a weight of zero. Even if a forward was to make a kick it would have no impact whatsoever on selection priority. Likewise, the weights for minutes played and tries are much lower for positions 1-3, these are specialist defensive positions and players rarely last a full 80 minutes.
This shows that there is a lot of flexibility in the model in order to incorporate subject matter expertise. There are 30 columns and 15 positions, meaning we have 450 preference options available to set between 0 and 1 on a continuous scale.
Figure 20 - Position Preference Weights Matrix
Figure 21 - Variable Preference Functions
In Figure 21 we can see the variable preference functions. We look to maximise variables such as Tries scored and Tackles Made whilst minimising handling errors and penalties.
The PROMETHEE II algorithm takes the inputs and builds a weighted preference matrix. These are then calculated as net flows from the positive and negative flows which look at pair-wise differences between candidate options. The positive flow is row wise sum divided by the number of candidates, and the negative flow is the column wise sum divided by the number of candidates in the preference matrix. Figure 22 shows an example of this in selecting the starting Number 8.
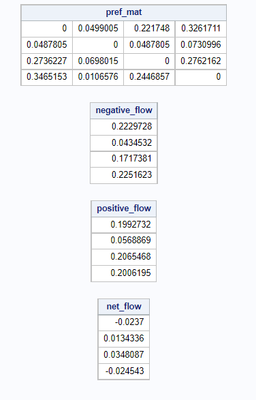
Figure 22 - Example of PROMETHEE Derived Preference Matrix
The algorithm then derives a rank score from the net flow, which is simply the element wise difference between the positive and negative flow. We can see in Figure 23 the output preferences for the candidate Number 8 players. This ranking will change as we update our preference weights.
Figure 23 - Example of PROMETHEE Selection for Number 8
Once the players have been ranked, the ranking outputs are merged and the ranks are standardised into a format that the minimum cost graph can solve. This simply takes the negative of the scaled preference rank score (scaled between 0 and 1) so that the absolute preferred player gets a score of -1 and the very least preferred gets a score of 0. The cost minimising graph solves the matching by matching players to positions 1-15 minimising the standardized rank score.
An example of this is shown in Figure 24, we can see several players are ranked first for more than one position (Courtney Lawes and Hamish Watson), the ranking will then assign these players to one of the positions such that the overall model cost is minimised (i.e. the most preferred second best will take the remaining position not filled by the person owning first place across the two positions).
Figure 24 - Standardized Rank Outputs
Figure 25 shows that the PROC OPTNET model is solved very quickly and returns an objective value, which is the minimum cost output. This objective value would also allow us to compare the efficiency of different model selections based on varying the analyst preference weights. However, we should be careful using this number to compare our models. It does not tell us how good the model is, simply how well the model is able to match players to positions in a way that minimised the standardised rank score (i.e. the model that best maximises the overall PROMETHEE rank based on model weights).
Figure 25 - PROC OPTNET Linear Assignment
We then re-run the above steps for the remaining players who were not selected for positions 1-15 in order to select our bench. in rugby the bench numbers relate to specific field positions.
Generally, the bench selection looks something like:
16=hooker
17=prop
18=prop
19=lock
20=loose forward
21=scrumhalf
22=flyhalf
23=utility back
For anyone reading this without an interest in rugby – apologies! The position naming is not always clear, for example a loose forward is a term used to describe positions 6,7 & 8 collectively, because they are loosely bound to the scrum.
Once we have re-ran the PROMETHEE ranking and minimum cost network graph for our bench we can then merge the two output datasets to view our selected team. Figure 26 shows one of the ‘neutral’ weight combinations I put together to select a balanced side. One thing to note is that Captain Alun Wyn Jones does not get selected, which is interesting. It is also interesting for this specific set of weights that Louis Rees-Zammit is selected on the starting line-up as well as several Saracens players. This is just one example of several team combinations the model picked based on the preference weights. You can see that for most players the number 1 ranked player is selected for the position, however in some positions the second best player (or even 3rd in the case of Josh Adams) are selected.
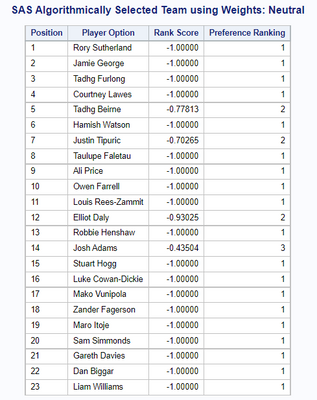
Figure 26 - Example Output of Model Selection
In the next, and final, article we explore the dataset before we begin building our model. Read Part 4 of the series here:
