MULTICOLLINEARITY SAS MACRO CODE

[#1]

Data miners deal with growing data size and dimensionality more often than not these days. As such, feature selection plays an increasingly crucial role as it improves predictive model interpretability, and helps to avoid overfitting and multicollinarity. Also, the speed of feature selection is very important when dealing with big data.

Variance inflation factor (VIF) regression is a fast algorithm that does feature selection in large regression problems. VIF regression handles a large number of features in a streamwise fashion. Streamwise regression method has its advantages over traditional stepwise regression because it offers faster computational speed without loss of accuracy. You can implement the VIF algorithm in SAS language using the SAS platform or server -- which usually stores big data sets.

For a more detailed explanation of the algorithm, please read my paper, VIF Regression: A SAS Application to Feature Selection in Large Data Sets. The paper includes SAS code that is used to implement the algorithm in the Appendix.

The VIF algorithm is essentially characterized by the following two components:

• The evaluation step approximates the partial correlation of each candidate variable with the response variable by correcting the marginal correlation using variance inflation factor (VIF), calculated from a small pre-sampled set.
• The search step tests each variable sequentially using an α-investing rule (Foster and Stine 2008). Variables are added only when they can reduce a statistically sufficient variance in the predictive model. The α-investing rule guarantees no model-overfitting and provides highly accurate models.

Table 1 uses pseudo-code to illustrate the VIF regression algorithm.

Table 1: VIF Regression Algorithm

This example uses the communities and crime data that are available in the UCI Machine Learning Repository. The data set consists of 2,215 observations on 125 predictors, and the regression model aims to predict the number of assaults in 1995. In the EM flow as shown in Figure 1, we make comparable analyses for stepwise regression, LARS and VIF regression. In the comparison, VIF regression and stepwise regression select similar numbers of variables, but the results from stepwise regression imply an overfitting problem. LARS yields the largest average squared error (ASE) in both training and validation data after 20 iteration steps.

Figure 1: Comparison Analysis Flow

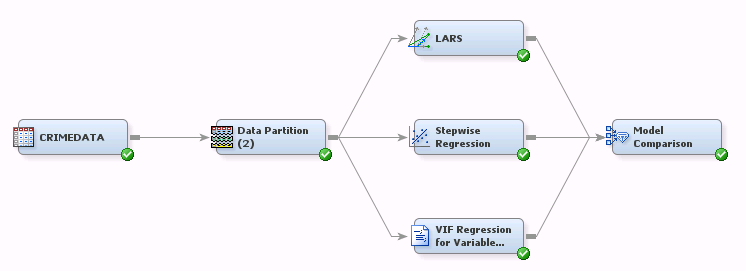
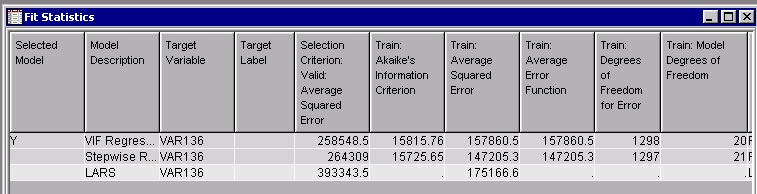
Figure 2 demonstrates that VIF regression outperforms the other two regression methods in terms of achieving the minimum average square error from validation. It selects 20 predictors in the setting of m=200, w0=0.05, Δw=0.05. Using AIC as a selection criterion, stepwise regression can scale down the set of predictors to 21, a little larger size than VIF regression; however, it suffers from overfitting. It has the smallest error in training data among all three methods, the second lowest is 157860.5. On the other hand, stepwise regression obtains an average square error that is obviously higher than VIF regression in validation data. LARS, in this example, has the largest error in both training and validation data.

Figure 2: Model Comparison Results

Multicollinearity is a known danger for causing overfitting in regression analysis. It produces large standard errors in the related independent variables and might introduce a large prediction error. Removing such data redundancy (variables with high correlation) improves statistical robustness for regression models.

VIF regression, which is based on VIF and fast robust estimates, is a streamwise regression approach to select variables. It has been proven to be an efficient algorithm in finding good subsets of variables from a huge space of candidates, and it can apply to online problems when features are generated and added to the model dynamically. You can see the SAS code that is used to implement the algorithm in the Appendix in the paper mentioned earlier.

[phullathi]

/* Author PRAKASH HULLATHI */
/*CREATING THE DATA FOR MULTICOLLINEARITY*/

%MACRO REMOVE_MULTICOLLINEARITY(DATASET=,YVAR=,VIF_CUTOFF=);

/*taking output of all variables*/
PROC CONTENTS DATA=&DATASET. VARNUM OUT=T;
RUN;

/*filter only numeric variables excluding dependent and date variables*/
DATA T1;
SET T;
KEEP NAME ;
WHERE TYPE=1 AND NAME NOT IN("&yvar.") and FORMAT not in('DATE') ;/* Remove target and date variables*/
RUN;

/*creating macro for independent variables*/
PROC SQL NOPRINT;
SELECT NAME INTO : XVARS SEPARATED BY ' '
FROM T1;
QUIT;

%PUT independent_variables=&XVARS;

/*running the regression model till independent variables vif< specified vif_cutoff*/
%DO %UNTIL (%SYSEVALF(&MAX_VIF.<=&VIF_CUTOFF.) );

/*taking the output of independent variables vif by removing the intercept*/
ODS OUTPUT PARAMETERESTIMATES=PAREST2;

PROC REG DATA=&DATASET. ;

MODEL &YVAR.= &XVARS. / VIF ;

RUN;

QUIT;

/*dropping the independent variables with missing vif value*/

DATA T11;
SET PAREST2;
IF VarianceInflation NOT IN(.) ;
RUN;

/*sorting the vif value by descending order*/
PROC SORT DATA=PAREST2 OUT=PAREST2_SORT ;
BY DESCENDING VarianceInflation;
RUN;

/*considering the highest vif value */
DATA PAREST2_SORT_2;
SET PAREST2_SORT;
IF _N_=1;
RUN;

/*creating the macro for highest vif value*/
PROC SQL NOPRINT;
SELECT VARIABLE INTO: REMOVE_VAR
FROM PAREST2_SORT_2;
QUIT;

/*dropping the highest vif value variable*/

PROC SQL NOPRINT ;
SELECT Variable INTO: XVARS SEPARATED BY ' '
FROM T11
WHERE VARIABLE NOT IN("&REMOVE_VAR.","Intercept") ;
QUIT;

/*getiing the highest vif value*/
PROC SQL NOPRINT;
SELECT MAX(VarianceInflation) INTO: MAX_VIF
FROM PAREST2;
QUIT;

%PUT max_vif=&MAX_VIF. variable_removed=&REMOVE_VAR. ;

%END;

%MEND REMOVE_MULTICOLLINEARITY;

%REMOVE_MULTICOLLINEARITY(DATASET=sashelp.cars,YVAR=MPG_City,VIF_CUTOFF=10)

/* after running the above sas macro code
for multicollinearity then run the below code */

/* final data set with no multicollinearity variables*/
data NO_MULTICOLLINEARITY;
SET PAREST2;
KEEP VARIABLE;
RUN;

PROC SQL NOPRINT;
SELECT VARIABLE INTO : XVARS_final SEPARATED BY ' '
FROM NO_MULTICOLLINEARITY
WHERE VARIABLE NOT IN("Intercept");
QUIT;

PROC REG DATA=SASHELP.CARS;
MODEL MPG_City=&XVARS_final./ VIF ;
RUN;
QUIT;

 PaigeMiller

Esteemed Advisor

Posts: 5,781

Re: MULTICOLLINEARITY SAS MACRO CODE

Options

Posted in reply to phullathi

Wednesday

Do you have a question? Or are you simply providing this macro for users of the Community?

Message 2 of 6 (152 Views)

Add Tag...

Quick ReplyReply

0 Likes

 phullathi

Occasional Contributor

Posts: 17

Re: MULTICOLLINEARITY SAS MACRO CODE

Options

Posted in reply to PaigeMiller

Wednesday

Hi Team,

This macro is for users

Regards
prakash hullathi

Message 3 of 6 (117 Views)

Add Tag...

Quick ReplyReply

0 Likes

 phullathi

Occasional Contributor

Posts: 17

Re: MULTICOLLINEARITY SAS MACRO CODE

Options

Posted in reply to phullathi

Wednesday

This sas macro is for users

Message 4 of 6 (126 Views)

Add Tag...

Quick ReplyReply

0 Likes

 phullathi

Occasional Contributor

Posts: 17

MULTICOLLINEARITY SAS MACRO CODE UPDATED [ Edited ]

Options

Posted in reply to phullathi

Thursday - last edited 3 hours ago

/* Author PRAKASH HULLATHI */
/*CREATING THE DATA FOR MULTICOLLINEARITY*/

%MACRO REMOVE_MULTICOLLINEARITY(DATASET=,YVAR=,VIF_CUTOFF=);

/*taking output of all variables*/
PROC CONTENTS DATA=&DATASET. VARNUM OUT=T;
RUN;

/*filter only numeric variables excluding dependent and date variables*/
DATA T1;
SET T;
KEEP NAME ;
WHERE TYPE=1 AND NAME NOT IN("&yvar.") and FORMAT not in('DATE') ;/* Remove target and date variables*/
RUN;

/*creating macro for independent variables*/
PROC SQL NOPRINT;
SELECT NAME INTO : XVARS SEPARATED BY ' '
FROM T1;
QUIT;

%PUT independent_variables=&XVARS;

/*running the regression model till independent variables vif< specified vif_cutoff*/
%DO %UNTIL (%SYSEVALF(&MAX_VIF.<=&VIF_CUTOFF.) );

/*taking the output of independent variables vif by removing the intercept*/
ODS OUTPUT PARAMETERESTIMATES=PAREST2;

PROC REG DATA=&DATASET. ;

MODEL &YVAR.= &XVARS. / VIF ;

RUN;

QUIT;

/*dropping the independent variables with missing vif value*/

DATA T11;
SET PAREST2;
IF VarianceInflation NOT IN(.) ;
RUN;

/*sorting the vif value by descending order*/
PROC SORT DATA=PAREST2 OUT=PAREST2_SORT ;
BY DESCENDING VarianceInflation;
RUN;

/*considering the highest vif value */
DATA PAREST2_SORT_2;
SET PAREST2_SORT;
IF _N_=1;
RUN;

/*creating the macro for highest vif value*/
PROC SQL NOPRINT;
SELECT VARIABLE INTO: REMOVE_VAR
FROM PAREST2_SORT_2;
QUIT;

/*dropping the highest vif value variable*/

PROC SQL NOPRINT ;
SELECT Variable INTO: XVARS SEPARATED BY ' '
FROM T11
WHERE VARIABLE NOT IN("&REMOVE_VAR.","Intercept") ;
QUIT;

/*getiing the highest vif value*/
PROC SQL NOPRINT;
SELECT MAX(VarianceInflation) INTO: MAX_VIF
FROM PAREST2;
QUIT;

%PUT max_vif=&MAX_VIF. variable_removed=&REMOVE_VAR. ;

%END;

%MEND REMOVE_MULTICOLLINEARITY;

%REMOVE_MULTICOLLINEARITY(DATASET=sashelp.cars,YVAR=MPG_City,VIF_CUTOFF=10)

/* after running the above sas macro code
for multicollinearity then run the below code */

/* final data set with no multicollinearity variables*/
data NO_MULTICOLLINEARITY;
SET PAREST2;
KEEP VARIABLE;
RUN;

PROC SQL NOPRINT;
SELECT VARIABLE INTO : XVARS_final SEPARATED BY ' '
FROM NO_MULTICOLLINEARITY
WHERE VARIABLE NOT IN("Intercept");
QUIT;

PROC REG DATA=SASHELP.CARS;
MODEL MPG_City=&XVARS_final./ VIF ;
RUN;
QUIT;

[#3]

/* Author PRAKASH HULLATHI */
/*CREATING THE DATA FOR MULTICOLLINEARITY*/

%MACRO REMOVE_MULTICOLLINEARITY(DATASET=,YVAR=,VIF_CUTOFF=);

/*taking output of all variables*/
PROC CONTENTS DATA=&DATASET. VARNUM OUT=T;
RUN;

/*filter only numeric variables excluding dependent and date variables*/
DATA T1;
SET T;
KEEP NAME ;
WHERE TYPE=1 AND NAME NOT IN("&yvar.") and FORMAT not in('DATE') ;/* Remove target and date variables*/
RUN;

/*creating macro for independent variables*/
PROC SQL NOPRINT;
SELECT NAME INTO : XVARS SEPARATED BY ' '
FROM T1;
QUIT;

%PUT independent_variables=&XVARS;

/*running the regression model till independent variables vif< specified vif_cutoff*/
%DO %UNTIL (%SYSEVALF(&MAX_VIF.<=&VIF_CUTOFF.) );

/*taking the output of independent variables vif by removing the intercept*/
ODS OUTPUT PARAMETERESTIMATES=PAREST2;

PROC REG DATA=&DATASET. ;

MODEL &YVAR.= &XVARS. / VIF ;

RUN;

QUIT;

/*dropping the independent variables with missing vif value*/

DATA T11;
SET PAREST2;
IF VarianceInflation NOT IN(.) ;
RUN;

/*sorting the vif value by descending order*/
PROC SORT DATA=PAREST2 OUT=PAREST2_SORT ;
BY DESCENDING VarianceInflation;
RUN;

/*considering the highest vif value */
DATA PAREST2_SORT_2;
SET PAREST2_SORT;
IF _N_=1;
RUN;

/*creating the macro for highest vif value*/
PROC SQL NOPRINT;
SELECT VARIABLE INTO: REMOVE_VAR
FROM PAREST2_SORT_2;
QUIT;

/*dropping the highest vif value variable*/

PROC SQL NOPRINT ;
SELECT Variable INTO: XVARS SEPARATED BY ' '
FROM T11
WHERE VARIABLE NOT IN("&REMOVE_VAR.","Intercept") ;
QUIT;

/*getiing the highest vif value*/
PROC SQL NOPRINT;
SELECT MAX(VarianceInflation) INTO: MAX_VIF
FROM PAREST2;
QUIT;

%PUT max_vif=&MAX_VIF. variable_removed=&REMOVE_VAR. ;

%END;

%MEND REMOVE_MULTICOLLINEARITY;

%REMOVE_MULTICOLLINEARITY(DATASET=sashelp.cars,YVAR=MPG_City,VIF_CUTOFF=10)

/* after running the above sas macro code
for multicollinearity then run the below code */

/* final data set with no multicollinearity variables*/
data NO_MULTICOLLINEARITY;
SET PAREST2;
KEEP VARIABLE;
RUN;

PROC SQL NOPRINT;
SELECT VARIABLE INTO : XVARS_final SEPARATED BY ' '
FROM NO_MULTICOLLINEARITY
WHERE VARIABLE NOT IN("Intercept");
QUIT;

PROC REG DATA=SASHELP.CARS;
MODEL MPG_City=&XVARS_final./ VIF ;
RUN;
QUIT;

[PaigeMiller]

Do you have a question? Or are you simply providing this macro for users of the Community?

[phullathi]

Hi Team,

This macro is for users

Regards
prakash hullathi

[phullathi]

This sas macro is for users

[phullathi]

/* Author PRAKASH HULLATHI */
/*CREATING THE DATA FOR MULTICOLLINEARITY*/

%MACRO REMOVE_MULTICOLLINEARITY(DATASET=,YVAR=,VIF_CUTOFF=);

/*taking output of all variables*/
PROC CONTENTS DATA=&DATASET. VARNUM OUT=T;
RUN;

/*filter only numeric variables excluding dependent and date variables*/
DATA T1;
SET T;
KEEP NAME ;
WHERE TYPE=1 AND NAME NOT IN("&yvar.") and FORMAT not in('DATE') ;/* Remove target and date variables*/
RUN;

/*creating macro for independent variables*/
PROC SQL NOPRINT;
SELECT NAME INTO : XVARS SEPARATED BY ' '
FROM T1;
QUIT;

%PUT independent_variables=&XVARS;

/*running the regression model till independent variables vif< specified vif_cutoff*/
%DO %UNTIL (%SYSEVALF(&MAX_VIF.<=&VIF_CUTOFF.) );

/*taking the output of independent variables vif by removing the intercept*/
ODS OUTPUT PARAMETERESTIMATES=PAREST2;

PROC REG DATA=&DATASET. ;

MODEL &YVAR.= &XVARS. / VIF ;

RUN;

QUIT;

/*dropping the independent variables with missing vif value*/

DATA T11;
SET PAREST2;
IF VarianceInflation NOT IN(.) ;
RUN;

/*sorting the vif value by descending order*/
PROC SORT DATA=PAREST2 OUT=PAREST2_SORT ;
BY DESCENDING VarianceInflation;
RUN;

/*considering the highest vif value */
DATA PAREST2_SORT_2;
SET PAREST2_SORT;
IF _N_=1;
RUN;

/*creating the macro for highest vif value*/
PROC SQL NOPRINT;
SELECT VARIABLE INTO: REMOVE_VAR
FROM PAREST2_SORT_2;
QUIT;

/*dropping the highest vif value variable*/

PROC SQL NOPRINT ;
SELECT Variable INTO: XVARS SEPARATED BY ' '
FROM T11
WHERE VARIABLE NOT IN("&REMOVE_VAR.","Intercept") ;
QUIT;

/*getiing the highest vif value*/
PROC SQL NOPRINT;
SELECT MAX(VarianceInflation) INTO: MAX_VIF
FROM PAREST2;
QUIT;

%PUT max_vif=&MAX_VIF. variable_removed=&REMOVE_VAR. ;

%END;

%MEND REMOVE_MULTICOLLINEARITY;

%REMOVE_MULTICOLLINEARITY(DATASET=sashelp.cars,YVAR=MPG_City,VIF_CUTOFF=10)

/* after running the above sas macro code
for multicollinearity then run the below code */

/* final data set with no multicollinearity variables*/
data NO_MULTICOLLINEARITY;
SET PAREST2;
KEEP VARIABLE;
RUN;

PROC SQL NOPRINT;
SELECT VARIABLE INTO : XVARS_final SEPARATED BY ' '
FROM NO_MULTICOLLINEARITY
WHERE VARIABLE NOT IN("Intercept");
QUIT;

PROC REG DATA=SASHELP.CARS;
MODEL MPG_City=&XVARS_final./ VIF ;
RUN;
QUIT;