LIME and ICE in SAS Viya 3.4: Interpreting Machine Learning Models

9 Likes

As computer power has increased, more and more complex machine learning models are feasible. The advantage of these models is that they can be highly accurate predictors. But a downside is that it can be difficult to explain how the results were achieved. In some cases, we may value accuracy over interpretability. In my opinion, self-driving cars or cybersecurity are domains where accuracy is highly valued. In other industries, like banking and finance, interpretability is valued, and regulations may even require a certain level of interpretability.

What if we could combine the best of both worlds? Use highly complicated and highly accurate models, but find ways to help interpret them? LIME, ICE, variable importance plots, and partial dependency plots all aim to help us interpret complex models.

Let’s define some terms. First, recall that there are many terms used to mean inputs and outputs.

Independent variable = input = feature = characteristic
Dependent variable = output = target = predicted outcome

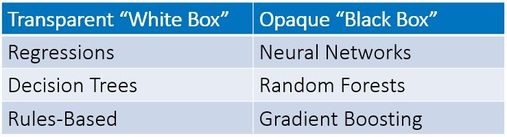
Black Boxes

The terms “black box” and “white box” are used to refer to less or more transparent models. There is generally a trade-off between interpretability and accuracy.

Results from “white box” (transparent) models can be easier to explain and interpret. The math from the independent variables may be relatively simple and it is often easy to see which independent variables are the most important in determining the dependent variable. However, we may relinquish some model accuracy.

Results from black box (opaque) models commonly have complex transformations. It may be hard to visualize and understand what is going on inside these models and it is usually difficult to communicate how why an individual record was scored as it was. However, the model results may be highly accurate.

A few examples of each type are shown below:

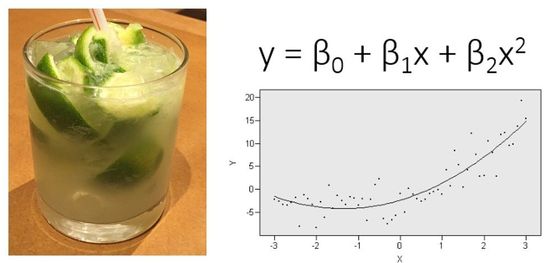
To break this down, I’ll use an analogy of the caipirinha (“white box”), versus a key lime pie (“black box”).

If we have a caipirinha, we can pretty much guess the ingredients:

lime
ice
sugar
cachaça

By looking and tasting, we can even venture a good guess about how much of each ingredient is included, and with one sip we can tell which ingredient seems to be dominant. Likewise, with linear regression or decision trees, we can fairly easily interpret our results. We can see which input variable is most important in determining our outcome.

This is analogous to our caipirinha. If we add too much cachaça, for example, we can’t find our car keys. Which is definitely for the best. Call Uber or Lyft. Hypothetically, I mean. But we know it was the cachaça and not the lime that created that outcome.

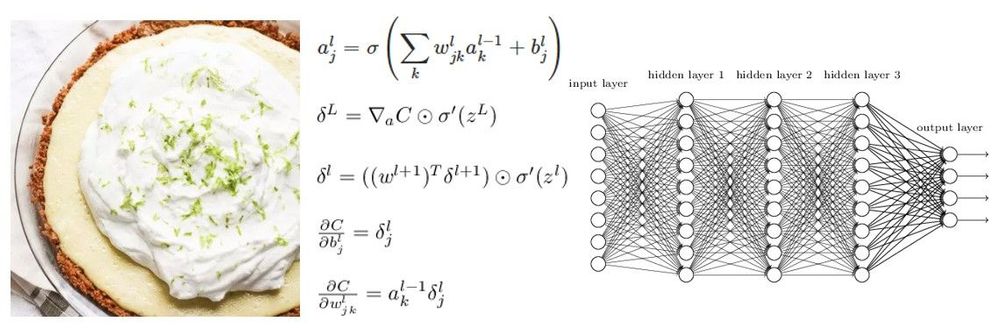
In contrast, let’s consider a key lime pie.

We happen to know that the ingredients for this key lime pie include:

condensed milk
sour cream
lime juice
lime zest
whipping cream
sugar
graham crackers
butter
eggs

But would we know this just by looking, or even taking a bite? Would we have even guessed that there are eggs are in the pie? Can we tell how much butter versus condensed milk versus sour cream versus whipping cream? What proportion of our slice is eggs? It’s very hard to tell, because the ingredients have been beaten, mixed and baked.

If our pie is the perfect flavor, but too soupy, what do we have to change? Less condensed milk? Less sour cream? Less whipping cream? Beat more? Beat less? It’s tricky.

But what if we could have our key lime pie and eat it, too?

Improving Interpretability of Black Box Models

There are some ways to improve the interpretability of black box models, including:

Using the results of a white box model (e.g., a decision tree) to help explain results
Include visualizations of inputs

Commonly, for interpretation, we are trying to explain the connection between inputs and outputs. For example, if someone is denied a loan, we may want to know what input factors were most important in influencing that denial.

Three methods that are model agnostic and visual and can be used to compare models are Variable Importance Rankings, LIME (Local Interpretable Model Agnostic Explanations), and ICE (Individual Conditional Expectation) plots. Partial Dependency Plots can also help us interpret complex models.

LIME, ICE Plots, and Partial Dependency Plots for model interpretability were added to in all supervised modeling nodes in Model Studio for VDMML 8.2.

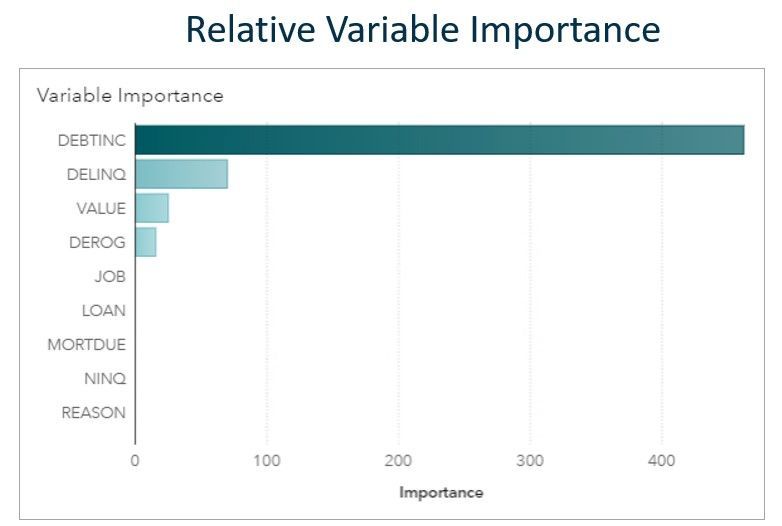
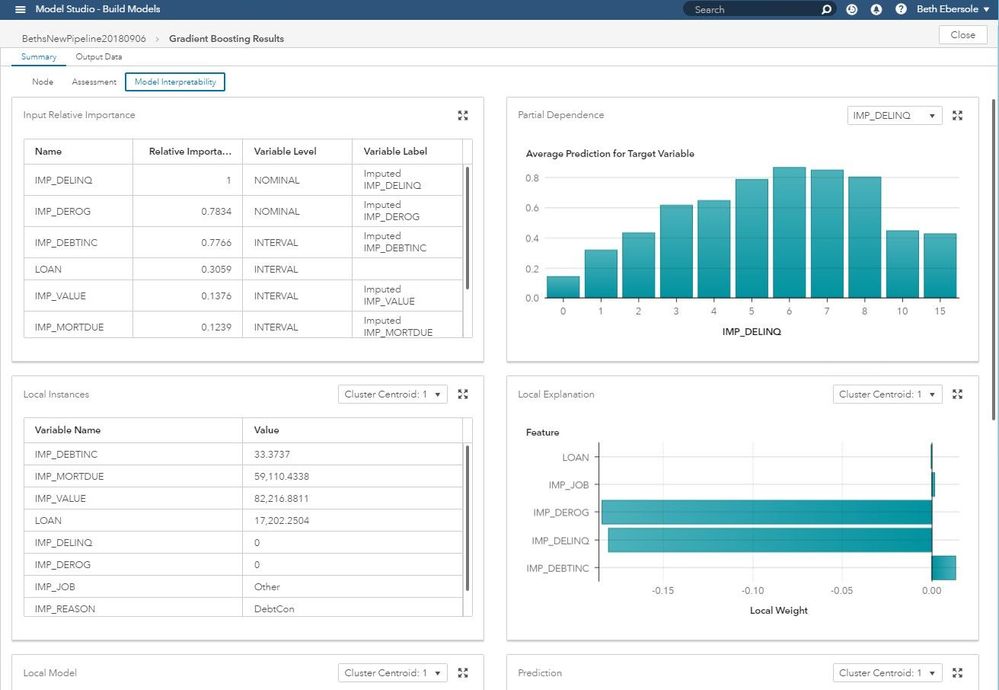
Variable Importance Rankings Plotted in a Bar Chart

Variable importance graphs:

Show you which variables are the most predictive in determining your outcome.
List input variable from most important to least important
Don’t tell you about the nature of the relationship between the independent variables and the dependent variable

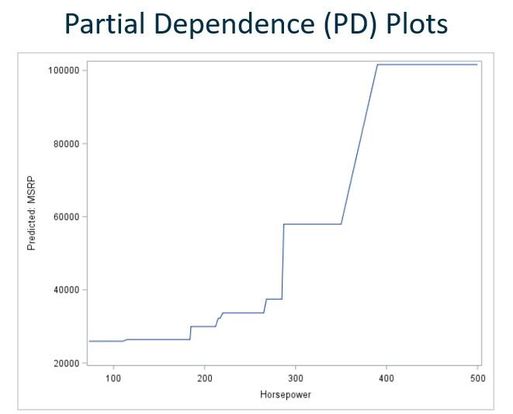
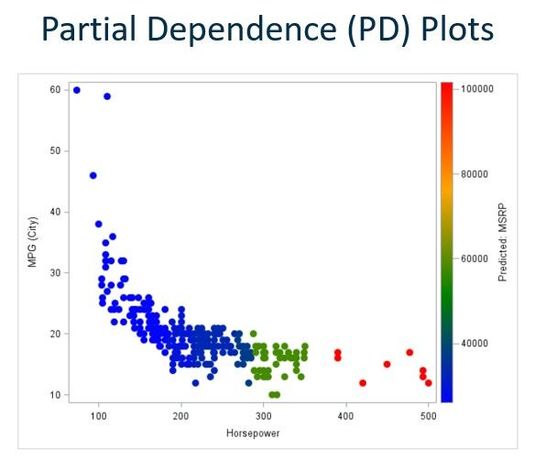
Partial Dependence Plots

Partial dependence plots show how values of model inputs affect the model’s predictions. A partial dependence plot in its simplest form shows how a single input (one independent variable) is related to the outcome (the dependent variable). This is illustrated above in the graph of manufacturer's suggested retail price (MSRP) by horsepower (from Ray Wright’s 2018 SGF paper Interpreting Black-Box Machine Learning Models Using Partial Dependence and Individual Conditional E...).

Both Partial Dependence and ICE plots are post hoc methods. They show how the model behaves in response to changing inputs.

CAUTION! The simplest partial dependency plot may not be meaningful if there are significant interaction effects among independent variables. Multi-way partial dependence plots can help you check for interactions.

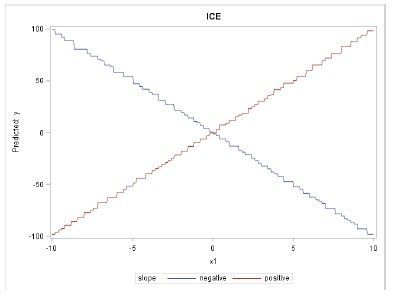
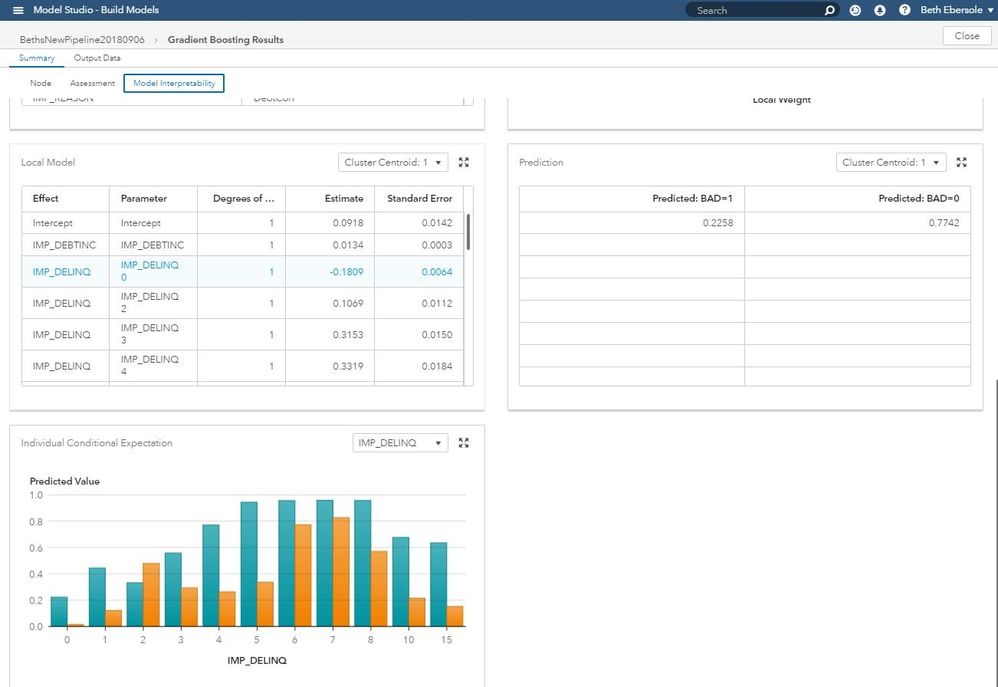
Individual Conditional Expectation (ICE) plots

ICE plots let you see visually how the inputs (independent variables) are related to the outcome (dependent variable). ICE curves can be understood as a “simulation that shows what would happen to the model’s prediction if you varied” one independent variable of a single observation. ICE plots are related to Partial Dependency plots, but they also let you find individual differences, subgroups of interest, and input interactions. Source.

In the first graph above, we see a PD plot that is essentially flat, indicating no relationship between the input X1 and the model predictions. When we look at the ICE plot on the right, however, we see two separate observations in the same data set, and we realize that the input X1 is strongly related to the target, but there are individual differences among observations.

To compute an ICE curve yourself, see Ray Wright’s 2018 SGF paper (also the source of the PD and ICE plot above).

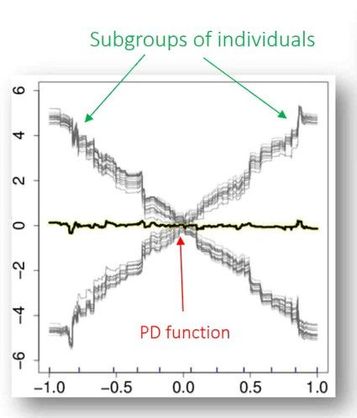
ICE plots were originally developed to display one curve for each observation from the training data set, but you can instead use sampling or clustering to reduce the number of curves to see patterns more easily. The ICE plot below by Andrew Christian illustrates using ICE plots to identify subgroups of individuals.

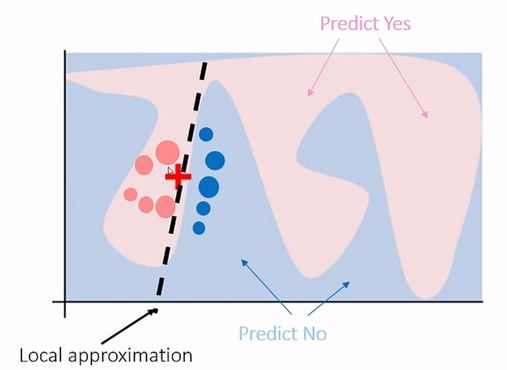
LIME: Local Interpretable Model Agnostic Explanations

LIME helps you to interpret an individual prediction/instance/point.

You start by selecting a particular instance (represented in graphic above by the red cross). Think of this instance as a cluster centroid.
Systematically adjust the inputs for that instance to generate more sample points around that point. In a binary outcome, for example, some will agree with the original outcome, some will have the opposite outcome.
These sample points now become new labeled training data for a simple linear regression model.
Calculate predictions for each of the sample points using your original training model (e.g., gradient boosting, neural network).
To focus on the most relevant part of the decision function, weight the sample points by their proximity to the original instance. Weight is represented in graph above by the size of the circle.
Use LASSO to determine the most important inputs.
Take those inputs and fit a linear model to describe a relationship between the perturbed inputs and outputs (shown as black dashed line above).

LIME explains the predictions of any classifier by fitting a linear regression to your original model inputs using prediction probability as the target.

Remember that the linear regression model here has PREDICTION PROBABILITY as its dependent variable, not your target, so it is not a representation of the variables that are important to your outcome. The LIME graphs represent the coefficients for the parameter estimates of the localized linear regression model. As a variable increases, it may have either a positive or negative effect on the PREDICTION for that cluster.

In SAS VDMML 8.3 (18w30), you could end up with a variable that’s predictive within the LIME model that is not represented in the actual model because the variables used in the linear regression model are selected using LASSO. In future releases, the linear model inputs will be limited to those inputs that are in the original model.

NOTE: Recall that LASSO (least absolute shrinkage and selection operator) is a shrinkage method in variable selection and regularization.

Still in VDMML 8.3 (18w25 release), LIME is calculated based on clusters (using k-prototypes clusters) rather than on individual observations. It chooses cluster centroids that serve as proxies for actual observations. Individual computation is on the roadmap.

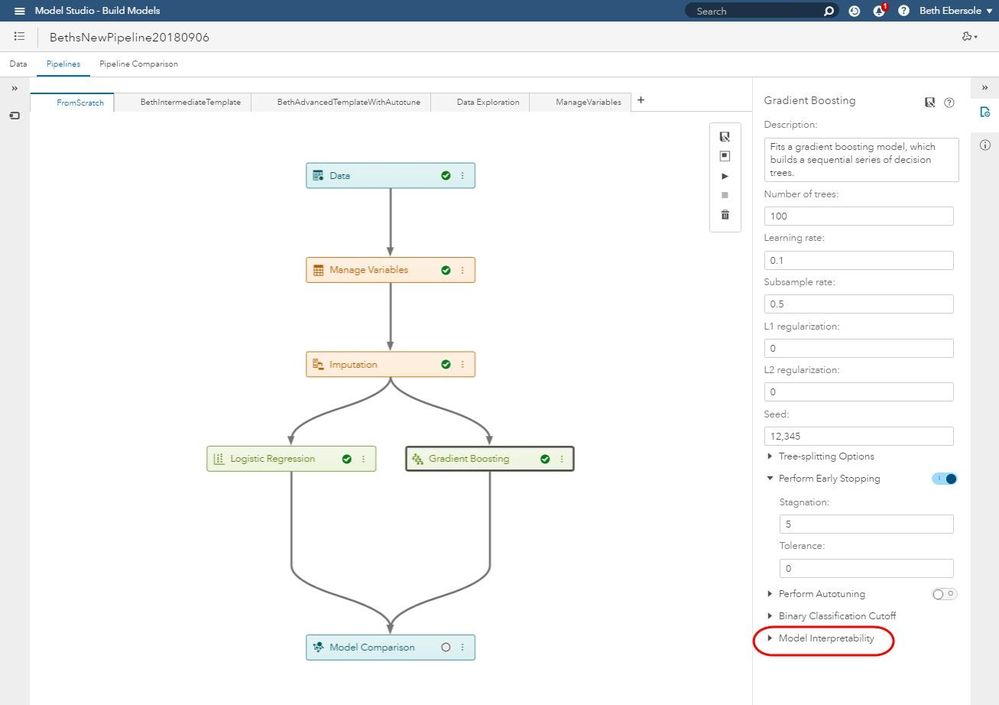
Interpretability Tools in Model Studio (VDMML 8.3)

In Model Studio (“Build Models”), you can select a model node, and you will see Model Interpretability in the right pane under the Node options, as shown below.

You can then expand Model Interpretability as shown below.

Example results are shown below.

REFERENCES and ADDITIONAL RESOURCES

Ilknur Kaynar Kabul’s article on AI and interpretability
Ilknur Kaynar Kabul’s June 12, 2018 article on interpreting model predictions with partial dependence and ICE plots
Introduction to Local Interpretable Model-Agnostic Explanations (LIME)
External SAS blogs
- Trusting AI Machine Learning
- Interpreting Data
Ilknur Kaynar-Kabul & Mustafa Kabul AI Webinar: Implementing AI Systems With Interpretability, Transparency and Trust (start at 34 minute mark)

Understanding Black-Box Models with Partial Dependence and Individual Conditional Expectation Plots
Documentation on Model Studio: SAS® Visual Data Mining and Machine Learning 8.3: Model Interpretabil...
LIME Python package
Marco Tulio Ribeiro, Sameer Singh, and Carlos Guestrin 2016 "Why Should I Trust You?": Explaining the Predictions of Any Classifier
Ray Wright’s paper Interpreting Black-Box Machine Learning Models Using Partial Dependence and Individual Conditional Expectation Plots, and video:

Since I wrote this article a couple of months ago, there have been a number of comments and tips regarding LIME and ICE on the Visual DMML listserv. A few of those are excerpted below:

Per Funda Gunes "You can get the score code of clustering from the “Model Interpretability” results. For this, make sure to click the “Create score code for assigning clusters” option under “Explain Individual Predictions.” It should not have a dependency on running a locally interpretable model (LIME). Once you have the score code, you can copy and paste it to a SAS Code node and run it for any partition of your data."
Per Funda Gunes: In the current version of VDMML (8.3) and Model Studio "By default, ICE plots are generated only for the top 3 most important variables. You can increase this number to 5 to make sure the default number of variables is same as LIME."

Ilknur Kaynar Kabul leads the SAS R&D team that creates tools for interpreting complex machine learning models. Much of the information in this post was extracted from resources she created.