- Home
- /
- SAS Communities Library
- /
- Best transformation – a new feature in SAS Model Studio 8.3
- RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
Best transformation – a new feature in SAS Model Studio 8.3
- Article History
- RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
Best transformation – what is it?
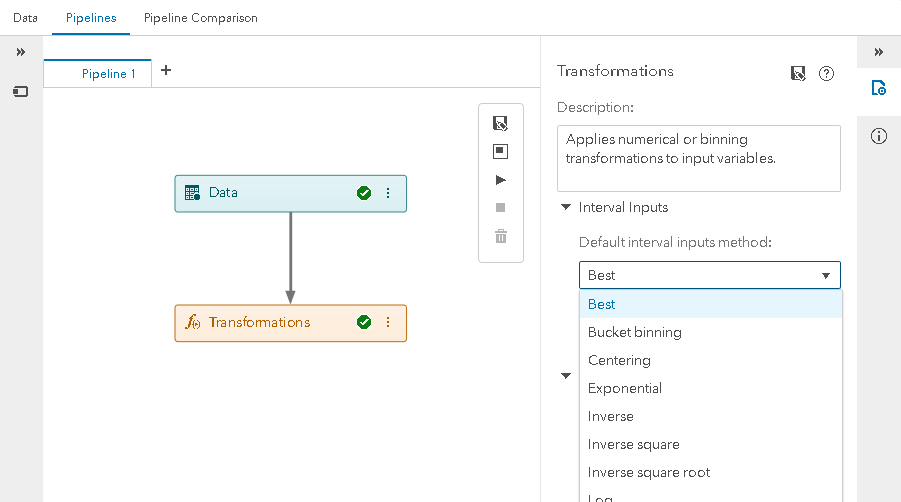
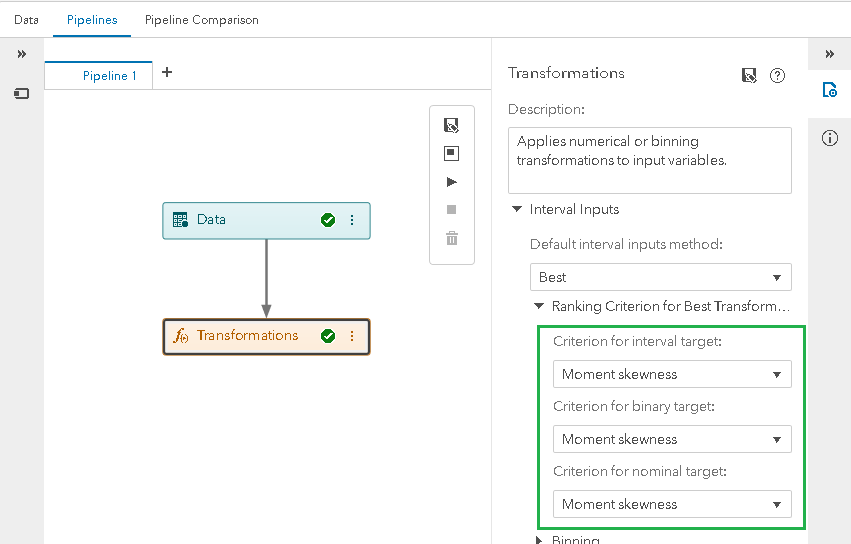
“Best” is not really a transformation, but a method or process to select the best transformation for an interval input. In the Transformations node (below), this method is accessed by selecting “Best” via the Default interval inputs method property. When specified, the Best method is applied to all interval inputs coming into the node, unless over-ridden by specific variable transformations identified in metadata via the Data tab or Manage Variables node (described below).
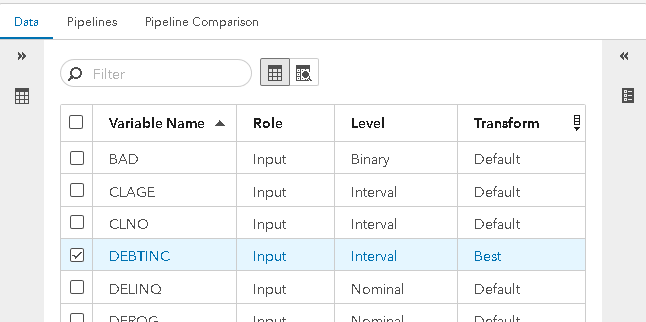
As a second option, for a project global setting, the Best transformation can be flagged for specific interval input variables on the Data tab. In the example below, the Best transformation is specified for the DEBTINC variable. That method will then be applied to DEBTINC when any Transformations node runs in the project.
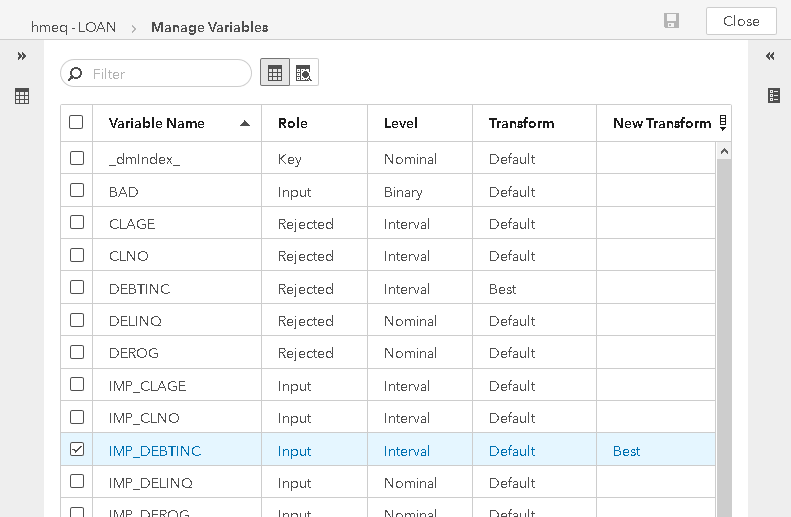
As a final option, the Best transformation can be flagged for a specific variable on a specific branch of a pipeline. This is done via the Manage Variables node. In the example below, the Manage Variables node is used to associate the Best transformation with the imputed variable IMP_DEBTINC. A succeeding Transformations node that is executed after this Manage Variables node will then apply the Best method to IMP_DEBTINC.
This is the list of transformations available through the Best method (with x representing the input variable):
- None – No transformation
- Centering – x minus its mean
- Inverse – 1/x
- Log – Natural log of x
- Log10 – Base 10 log of x
- Square – x squared
- Square root – Square root of x
- Inverse square – 1/(x squared)
- Inverse square root – 1/(Square root of x)
- Range standardization – x transformed onto the range 0 to 1
- Standardization – x standardized using its Mean and StdDev
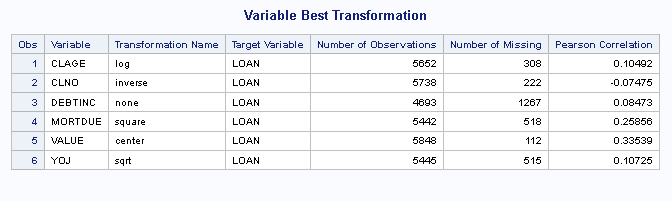
When processing the Best transformation for an input variable, the list of available transformations is applied, and the resulting values are analyzed to determine the best transformation based on a ranking criterion (I discuss this in the next section). Below is an example report which shows the list of input variables with their selected transformations. In this example, the Pearson correlation coefficient is the ranking criterion.
Best transformation – how does it work?
As I briefly explain in the previous section, the best transformation for an interval input is determined by using a ranking criterion. Below is a listing of the available ranking criteria broken into three groups:
Univariate statistics (all target types)
- Moment skewness
- Average quantile skewness
- Moment kurtosis
- Average quantile kurtosis
Empirical distribution comparison statistics (binary target)
- Anderson-Darling statistic with target
- Cramer-Von Mises statistic with target
- Kolmogorov-Smirnov statistic (K-S) with target
Correlation statistics (interval target)
- Pearson correlation with target
Univariate statistics – The four univariate statistics are used to select the transformation that maximizes a normal distribution for an input, which in all cases is the transformation whose absolute value of the statistic is closest to zero. The average quantile statistics (average quantile skewness, average quantile kurtosis) use ratios of average quantile values in their formulas. They are considered robust, as they are significantly less sensitive to extreme outliers. For further documentation on the average quantile statistics, see the article http://www.cirano.qc.ca/realisations/grandes_conferences/methodes_econometriques/white.pdf . From the article: The average quantile skewness is SK3= (m-Q2)/(AAD_median), multiplied by 3. The average quantile kurtosis is KR3=((U0.05 – L0.05)/(U0.5 – L0.5)) – 2.59.
Empirical distribution comparison statistics – These three statistics are used to compare the empirical distributions of a transformed input between the binary target groups. The potential input predictive power increases with a greater distribution variation between the groups. For all three statistics, the transformation with the greatest distribution variation is that which has the maximum statistic value, and that is the transformation that is selected.
Correlation statistics – For each interval input, the Pearson correlation coefficient measures the linear correlation between each transformed input and the target. The transformation with the highest correlation statistic is selected.
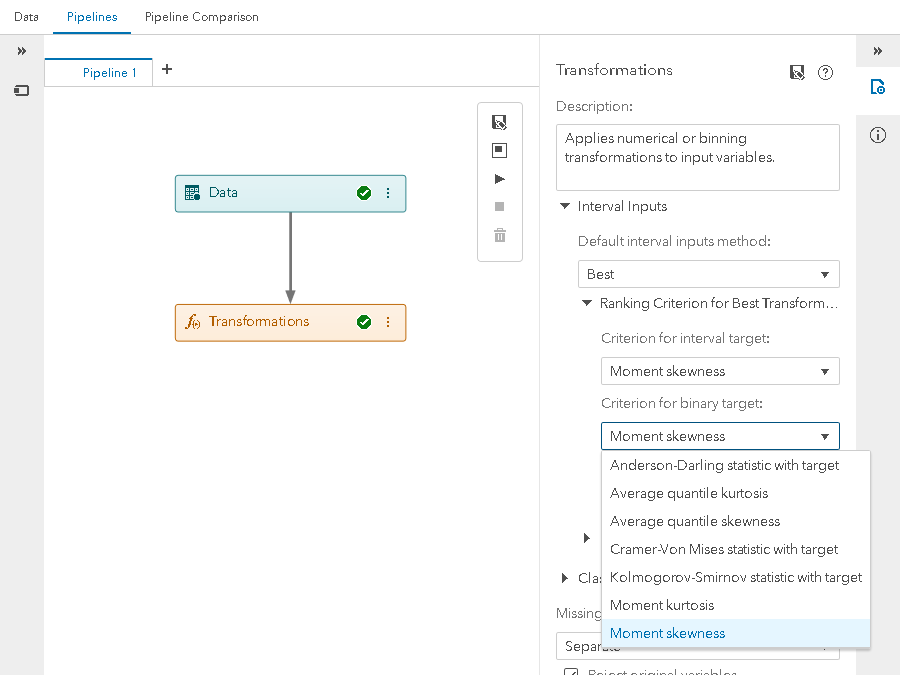
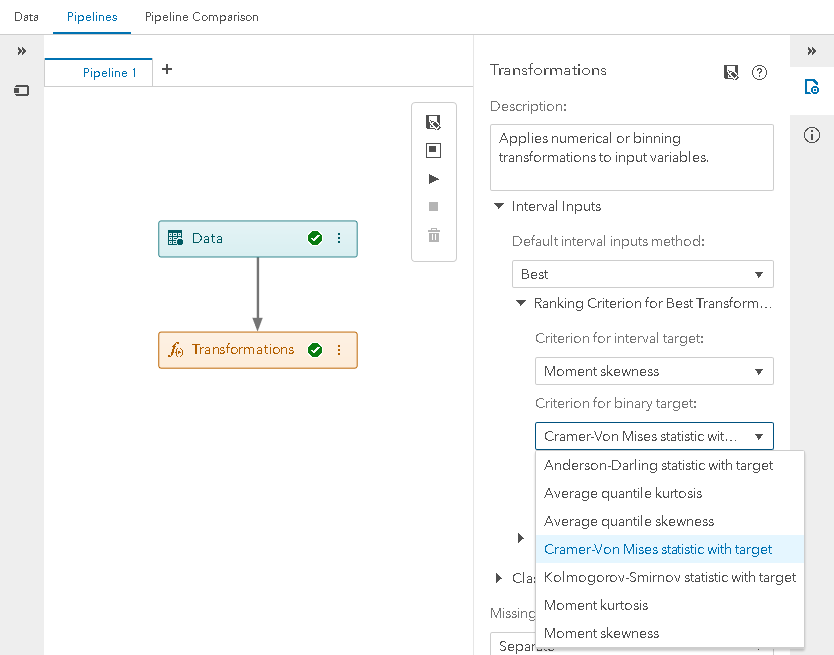
To be able to select a ranking criterion for the Best transformation process, we have added three new properties to the Transformations node, located within the Ranking Criterion for Best Transformation group: Criterion for interval target, Criterion for binary target, and Criterion for nominal target.
The criteria are broken out into these three properties. The property to use depends upon the level of the target variable (Interval, Binary, or Nominal) in your data. Each property is a pull-down selector which defaults to “Moment skewness”. Note: Since the univariate statistics don’t use the target, these four statistics are available in all three properties.
Criterion for interval target – In addition to the univariate statistics, this property includes the Pearson correlation statistic.
- Average quantile kurtosis
- Average quantile skewness
- Moment kurtosis
- Moment skewness
- Pearson correlation with target
Criterion for binary target – In addition to the univariate statistics, this property includes the empirical distribution comparison statistics.
- Anderson-Darling statistic with target
- Average quantile kurtosis
- Average quantile skewness
- Cramer-Von Mises statistic with target
- Kolmogorov-Smirnov statistic with target
- Moment kurtosis
- Moment skewness
Criterion for nominal target (non-binary) – This property includes the univariate statistics.
- Average quantile kurtosis
- Average quantile skewness
- Moment kurtosis
- Moment skewness
Let’s use home equity data (HMEQ) as an example. Hmeq is in the Sampsio library that SAS provides, accessible through SAS® Studio. It contains credit line information for mortgage applicants, such as debt-to-income ratio, requested loan amount, number of credit lines, etc. For the Transformations node, I first set the default interval inputs method to “Best”, and since our target is binary variable BAD, I use the property Criterion for binary target. For this first example, I run with the default value, “Moment skewness” (below).
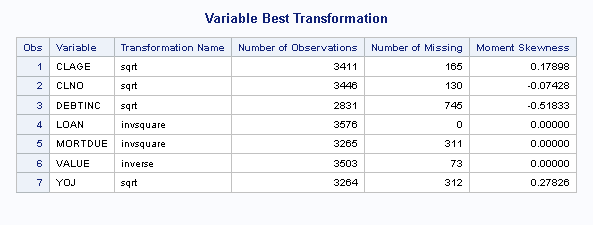
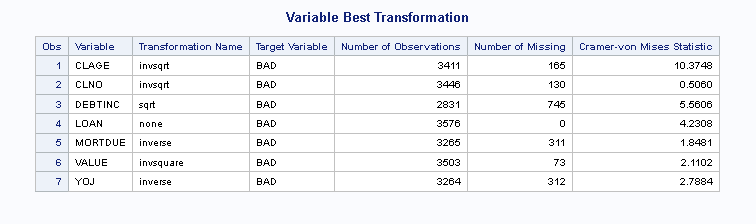
In the node results output, the Variable Best Transformation report provides the selected transformation for each variable and the skewness value for each.
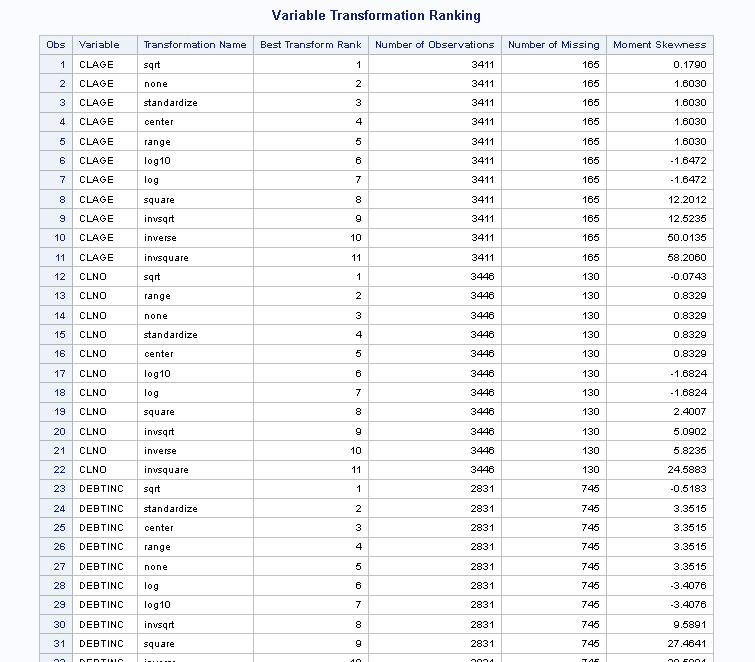
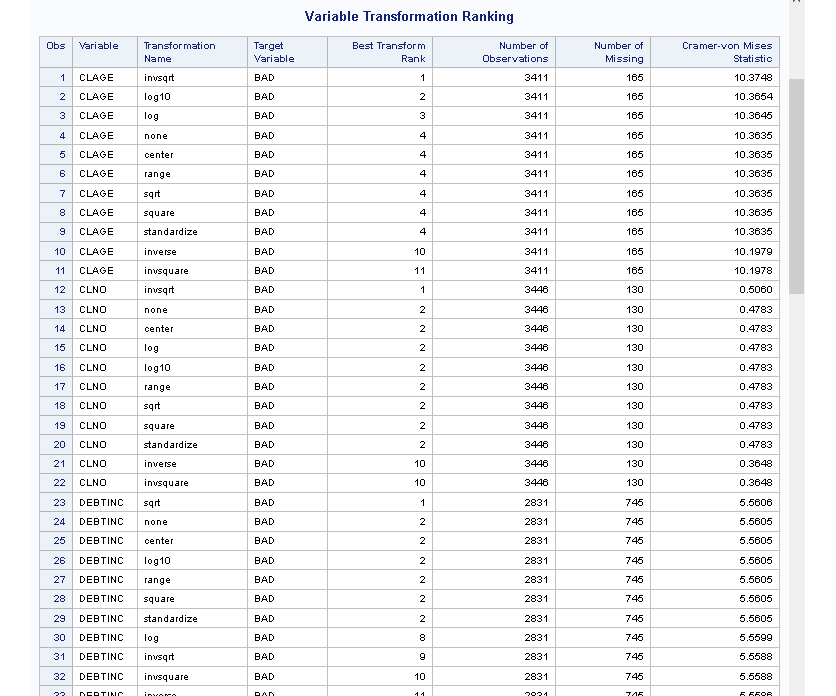
In the same output results, the Variable Transformation Ranking report provides the full ranking results for all the transformations. The selected transformations have a rank of 1.
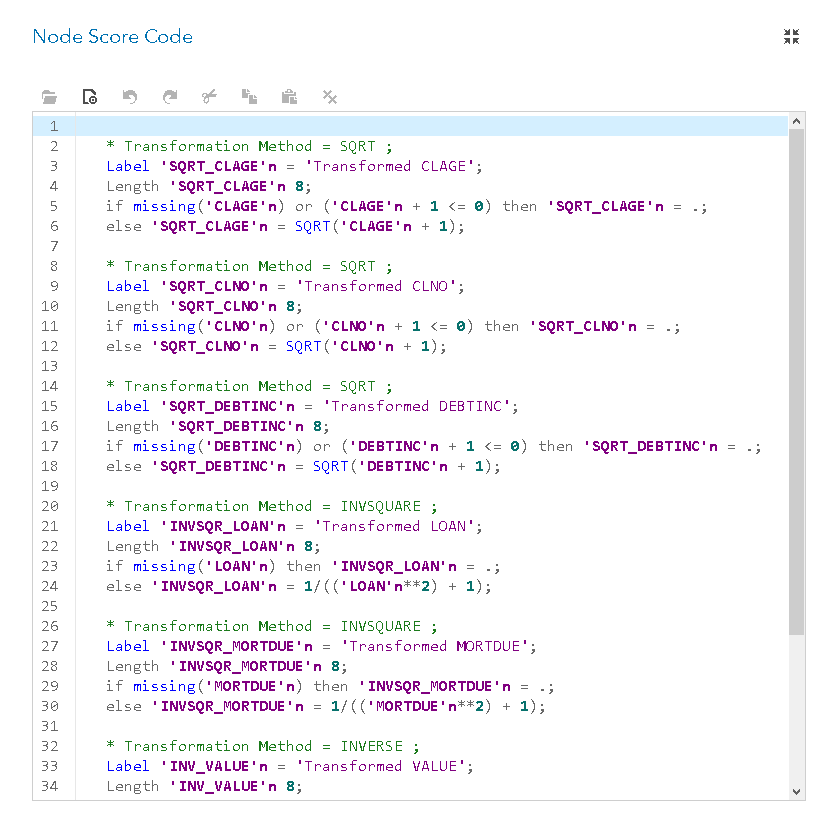
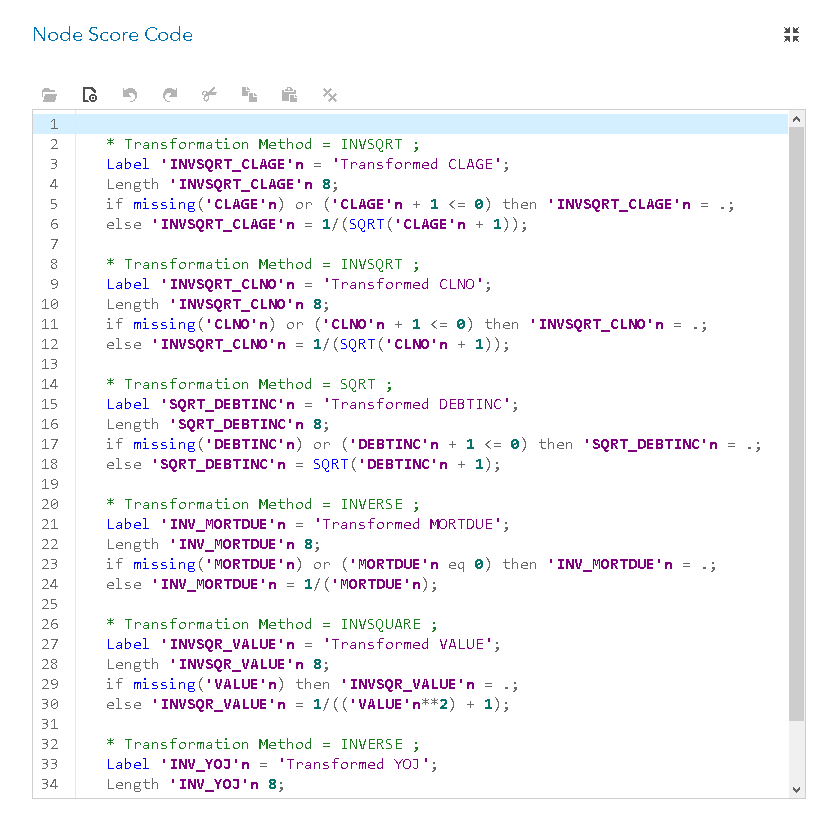
In the node score code, you can confirm that the selected transformations are used.
For the second example, I run with the Cramer-Von Mises statistic:
The selected transformations are in the Variable Best Transformation report:
In the Variable Transformation Ranking report, you can see that the transformations with the maximum Cramer-von Mises Statistic have a rank of 1, and these are the transformations that are selected.
The node score code confirms that the selected transformations are used:
Summary
In this article, I have given an overview of the Best transformation method, and I have provided examples to illustrate how it’s used. Here are the main points:
- Best is a method used in the Transformations node to select, using a specified ranking criterion, the highest ranking transformation for an interval input.
- The highest ranking transformation provides the most normal distribution, the most predictive power based upon distribution variation between target groups, or the highest correlation to an interval target.
- The available ranking criteria are broken-out into three new properties by the type of target in your data (Interval, Binary, or Nominal).
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Report Inappropriate Content
Excellent explanation, awesome.
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and lock in 2025 pricing—just $495!
SAS AI and Machine Learning Courses
The rapid growth of AI technologies is driving an AI skills gap and demand for AI talent. Ready to grow your AI literacy? SAS offers free ways to get started for beginners, business leaders, and analytics professionals of all skill levels. Your future self will thank you.