- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hello, I'm a very new SAS user and would like to know if there is any solution to the problem I am facing. I have read through many questions regarding replicating Solver in excel and most of them require SAS/OR, which I unfortunately don't have access to. Is there any way to achieve the same result without PROC OPTMODEL?
Please see the attached file for details of the problem.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
With OPTMODEL:
data indata;
input Weight Probability;
Probability = Probability / 100;
datalines;
2 0.001
34 0.010
56 0.030
90 0.070
27 0.120
10 1.100
;
proc optmodel;
set OBS;
num weight {OBS};
num probability {OBS};
read data indata into OBS=[_N_] weight probability;
num logit {i in OBS} = log(probability[i]/(1-probability[i]));
print weight probability logit;
var X;
impvar OptimizedLogit {i in OBS} = logit[i] + X;
impvar OptimizedProbability {i in OBS} = 1/(1+exp(-OptimizedLogit[i]));
impvar WeightedAverage = (sum {i in OBS} weight[i] * OptimizedProbability[i]) / (sum {i in OBS} weight[i]);
num target = 0.003;
min Error = abs(WeightedAverage - target);
solve with nlp / ms;
print X WeightedAverage OptimizedLogit OptimizedProbability;
quit;| Solution Summary | |
|---|---|
| Solver | Multistart NLP |
| Algorithm | Interior Point Direct |
| Objective Function | Error |
| Solution Status | Best Feasible |
| Objective Value | 6.505213E-17 |
| Number of Starts | 100 |
| Number of Sample Points | 320 |
| Number of Distinct Optima | 73 |
| Random Seed Used | 7412291 |
| Optimality Error | 0.0029506036 |
| Infeasibility | 0 |
| Presolve Time | 0.00 |
| Solution Time | 0.05 |
| X | WeightedAverage |
|---|---|
| 1.0799 | 0.003 |
| [1] | OptimizedLogit | OptimizedProbability |
|---|---|---|
| 1 | -10.4331 | 0.000029442 |
| 2 | -8.1304 | 0.000294370 |
| 3 | -7.0316 | 0.000882766 |
| 4 | -6.1839 | 0.002058189 |
| 5 | -5.6444 | 0.003524902 |
| 6 | -3.4189 | 0.031708828 |
With DATA step, using discrete steps on interval [0,2]:
%let numObs = 6;
data sample;
array Weight[&numObs] (2 34 56 90 27 10);
array Probability[&numObs] (0.00001 0.0001 0.0003 0.0007 0.0012 0.011);
array Logit[&numObs];
SumOfWeights = sum(of Weight[*]);
do i = 1 to &numObs;
Logit[i] = log(Probability[i]/(1-Probability[i]));
end;
array OptimizedLogit[&numObs];
array OptimizedProbability[&numObs];
do X = 0 to 2 by 0.01;
WeightedAverage = 0;
do i = 1 to &numObs;
OptimizedLogit[i] = Logit[i] + X;
OptimizedProbability[i] = 1/(1+exp(-OptimizedLogit[i]));
WeightedAverage + Weight[i] * OptimizedProbability[i];
end;
WeightedAverage = WeightedAverage / SumOfWeights;
output;
end;
run;
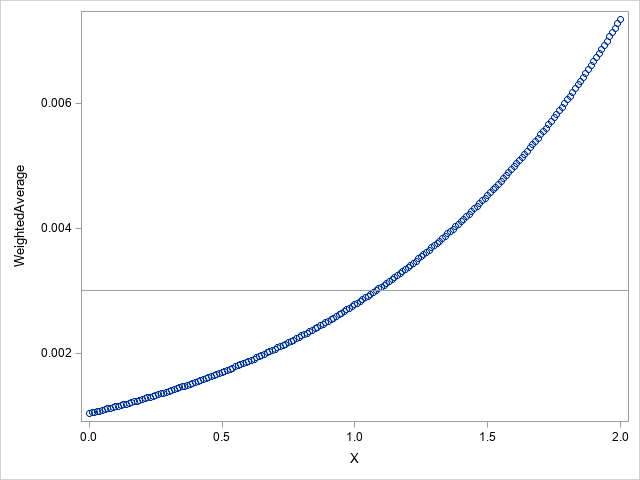
proc sgplot data=sample;
scatter x=X y=WeightedAverage;
refline 0.003;
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
With OPTMODEL:
data indata;
input Weight Probability;
Probability = Probability / 100;
datalines;
2 0.001
34 0.010
56 0.030
90 0.070
27 0.120
10 1.100
;
proc optmodel;
set OBS;
num weight {OBS};
num probability {OBS};
read data indata into OBS=[_N_] weight probability;
num logit {i in OBS} = log(probability[i]/(1-probability[i]));
print weight probability logit;
var X;
impvar OptimizedLogit {i in OBS} = logit[i] + X;
impvar OptimizedProbability {i in OBS} = 1/(1+exp(-OptimizedLogit[i]));
impvar WeightedAverage = (sum {i in OBS} weight[i] * OptimizedProbability[i]) / (sum {i in OBS} weight[i]);
num target = 0.003;
min Error = abs(WeightedAverage - target);
solve with nlp / ms;
print X WeightedAverage OptimizedLogit OptimizedProbability;
quit;| Solution Summary | |
|---|---|
| Solver | Multistart NLP |
| Algorithm | Interior Point Direct |
| Objective Function | Error |
| Solution Status | Best Feasible |
| Objective Value | 6.505213E-17 |
| Number of Starts | 100 |
| Number of Sample Points | 320 |
| Number of Distinct Optima | 73 |
| Random Seed Used | 7412291 |
| Optimality Error | 0.0029506036 |
| Infeasibility | 0 |
| Presolve Time | 0.00 |
| Solution Time | 0.05 |
| X | WeightedAverage |
|---|---|
| 1.0799 | 0.003 |
| [1] | OptimizedLogit | OptimizedProbability |
|---|---|---|
| 1 | -10.4331 | 0.000029442 |
| 2 | -8.1304 | 0.000294370 |
| 3 | -7.0316 | 0.000882766 |
| 4 | -6.1839 | 0.002058189 |
| 5 | -5.6444 | 0.003524902 |
| 6 | -3.4189 | 0.031708828 |
With DATA step, using discrete steps on interval [0,2]:
%let numObs = 6;
data sample;
array Weight[&numObs] (2 34 56 90 27 10);
array Probability[&numObs] (0.00001 0.0001 0.0003 0.0007 0.0012 0.011);
array Logit[&numObs];
SumOfWeights = sum(of Weight[*]);
do i = 1 to &numObs;
Logit[i] = log(Probability[i]/(1-Probability[i]));
end;
array OptimizedLogit[&numObs];
array OptimizedProbability[&numObs];
do X = 0 to 2 by 0.01;
WeightedAverage = 0;
do i = 1 to &numObs;
OptimizedLogit[i] = Logit[i] + X;
OptimizedProbability[i] = 1/(1+exp(-OptimizedLogit[i]));
WeightedAverage + Weight[i] * OptimizedProbability[i];
end;
WeightedAverage = WeightedAverage / SumOfWeights;
output;
end;
run;
proc sgplot data=sample;
scatter x=X y=WeightedAverage;
refline 0.003;
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thank you for your reply. However I'm still unsure of how to get X as an output without proc optmodel. Is eyeballing the graph the only way to get X with this method?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You can examine the resulting data set to find that X = 1.08 yields WeightedAverage = 0.0030004091.
Various other ways to solve nonlinear equations in SAS are described in the blog post https://blogs.sas.com/content/iml/2018/02/28/solve-system-nonlinear-equations-sas.html
SAS Innovate 2025: Save the Date
SAS Innovate 2025 is scheduled for May 6-9 in Orlando, FL. Sign up to be first to learn about the agenda and registration!
Learn how to run multiple linear regression models with and without interactions, presented by SAS user Alex Chaplin.
Find more tutorials on the SAS Users YouTube channel.