- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
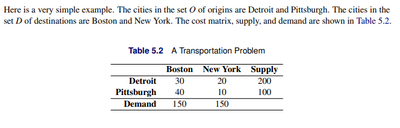
I'm working through a problem I'm trying to solve using proc optmodel and I found an example (see page 12 "A Transportation Problem") from the SAS sample library on the optmodel procedure that is close to what I'm trying to do. I'm struggling to replace the hard-coded values in the red code below with values from datasets (costs, supply, and demand)
proc optmodel;
/* specify parameters */
set O={'Detroit','Pittsburgh'};
set D={'Boston','New York'};
number c{O,D}=[30 20
40 10];
number a{O}=[200 100];
number b{D}=[150 150];
/* model description */
var x{O,D} >= 0;
min total_cost = sum{i in O, j in D}c[i,j]*x[i,j];
constraint supply{i in O}: sum{j in D}x[i,j]=a[i];
constraint demand{j in D}: sum{i in O}x[i,j]=b[j];
/* solve and output */
solve;
print x;
Below is the "input" table given in the example:
I have seen other optmodel examples that read values from datasets, but the key for me is I need my output in this matrix format where I can get the optimum configurations by origination and destination.
@RobPratt I'm hoping you can help me, based on my many hours of google searches looks like you're an absolute GOAT on optmodel! 😁
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The following reads from your three data sets, solves the problem, and creates two output data sets: one in sparse form like your costs data set, and one in dense matrix form, like you requested. Note the use of the COMPRESS function because New York is not a valid data set variable name.
proc optmodel;
/* specify parameters */
set <str> O;
set <str> D;
number c{O,D};
number a{O};
number b{D};
/* read data */
read data supply into O=[origination] a=supply;
read data demand into D=[destination] b=demand;
read data costs into [origination destination] c=cost;
/* model description */
var x{O,D} >= 0;
min total_cost = sum{i in O, j in D}c[i,j]*x[i,j];
constraint supply{i in O}: sum{j in D}x[i,j]=a[i];
constraint demand{j in D}: sum{i in O}x[i,j]=b[j];
/* solve and output */
solve;
print x;
/* create data */
create data sparse from [origination destination] x;
create data dense from [origination]=O {j in D} <col(compress(j))=x[origination,j]>;
quit;- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I would be glad to help. Please share your data sets.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Wow, thank you so much Rob. I just translated the example into 3 datasets -- here they are:
data costs;
length origination $25. destination $25. cost 8;
input origination & destination & cost;
cards;
Detroit Boston 30
Detroit New York 20
Pittsburgh Boston 40
Pittsburgh New York 10
;
data supply;
length origination $25. supply 8;
input origination & supply;
cards;
Detroit 200
Pittsburgh 100
;
data demand;
length destination $25. demand 8;
input destination & demand;
cards;
Boston 150
New York 150
;- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The following reads from your three data sets, solves the problem, and creates two output data sets: one in sparse form like your costs data set, and one in dense matrix form, like you requested. Note the use of the COMPRESS function because New York is not a valid data set variable name.
proc optmodel;
/* specify parameters */
set <str> O;
set <str> D;
number c{O,D};
number a{O};
number b{D};
/* read data */
read data supply into O=[origination] a=supply;
read data demand into D=[destination] b=demand;
read data costs into [origination destination] c=cost;
/* model description */
var x{O,D} >= 0;
min total_cost = sum{i in O, j in D}c[i,j]*x[i,j];
constraint supply{i in O}: sum{j in D}x[i,j]=a[i];
constraint demand{j in D}: sum{i in O}x[i,j]=b[j];
/* solve and output */
solve;
print x;
/* create data */
create data sparse from [origination destination] x;
create data dense from [origination]=O {j in D} <col(compress(j))=x[origination,j]>;
quit;- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Rob -- I hate to ask again but my needs have slightly changed. In the below example I'm trying to solve a problem where I have more customer orders than I can fill for different product lines. I'd like to be able to maximize revenue and fill at least 10% of each customer's orders (where possible). I must not be understanding the array aspect of reading data into the optmodel procedure, what do I have incorrect below?
Thanks @RobPratt!
data orders_costs;
length customer $25. product $25. revenue 8. num_orders 8.;
input customer & product & revenue num_orders;
cards;
CustomerA ProductA 300 100
CustomerA ProductB 200 130
CustomerB ProductA 300 0
CustomerB ProductB 200 10
CustomerC ProductA 300 10
CustomerC ProductB 200 60
;
data supply;
length product $25. supply 8;
input product & supply;
cards;
ProductA 85
ProductB 180
;
data demand;
length product $25. demand 8;
input product & demand;
cards;
ProductA 110
ProductB 200
;
/*Note: optimum_orders_to_fill is hypothetical*/
data want;
length customer $25. product $25. optimum_orders_to_fill 8. num_orders 8.;
input customer & product & optimum_orders_to_fill num_orders;
cards;
CustomerA ProductA 84 100
CustomerA ProductB 120 130
CustomerB ProductA 0 0
CustomerB ProductB 5 10
CustomerC ProductA 1 10
CustomerC ProductB 55 60
;
proc optmodel;
/* declare sets and data indexed by sets */
set <str> O;
set <str> D;
number a{O};
number b{D};
number c{O,D};
number n{O,D};
/* read data */
read data supply into O=[product] a=supply; /*supply*/
read data orders_costs into D=[customer] b=num_orders; /*customer product demand*/
read data orders_costs into [customer product] c=revenue; /*revenue*/
read data orders_costs into [customer product] n=num_orders; /*customer demand*/
/* solve variable and model description */
/*matrix of supply and demand*/
var x{O,D} >= 0;
/*model objective*/
max total_revenue = sum{i in O, j in D}c[i,j]*x[i,j];
/*constraints*/
constraint supply{i in O}: sum{j in D}x[i,j]=a[i];
constraint demand{j in D}: sum{i in O}x[i,j]=b[j];
/*ability to add constraint where each customer has at least 10% of their orders filled?*/
/* solve and output */
solve;
print x;
/* create data */
create data sparse from [customer product] x;
create data dense from [product]=O {j in D} <col(j)=x[product,j]>;
quit;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You have the indices reversed in the last two READ DATA statements. Also, you can merge them into one statement:
read data orders_costs into [product customer] c=revenue n=num_orders;
This change will get you past the error, but now your problem is infeasible because total supply does not equal total demand. To instead fill at least 10% of demand, you can modify your demand constraint as follows:
constraint demand{j in D}: sum{i in O}x[i,j] >= 0.1*b[j];
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
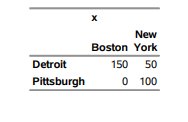
Thanks Rob -- I'm not sure if the updated demand constraint is working correctly. I'm expecting at least 10% of a customer's orders to be filled up until the supply constraint runs out.
For example, in my data CustomerA has placed 100 orders for ProductA and CustomerC has placed 10 orders. Total supply for ProductA is 85, and demand is 110.
The solver outputs the below result which is strange since in this simple example the revenue is the same for this product I would expect to see something like 84 units for CustomerA and 1 unit for CustomerC.
data orders_costs;
length customer $25. product $25. revenue 8. num_orders 8.;
input customer & product & revenue num_orders;
cards;
CustomerA ProductA 300 100
CustomerA ProductB 200 130
CustomerB ProductA 300 0
CustomerB ProductB 200 10
CustomerC ProductA 300 10
CustomerC ProductB 200 60
;
data supply;
length product $25. supply 8;
input product & supply;
cards;
ProductA 85
ProductB 180
;
data demand;
length product $25. demand 8;
input product & demand;
cards;
ProductA 110
ProductB 200
;
proc optmodel;
/* declare sets and data indexed by sets */
set <str> O;
set <str> D;
number a{O};
number b{D};
number c{O,D};
number n{O,D};
/* read data */
read data supply into O=[product] a=supply; /*supply*/
read data orders_costs into D=[customer] b=num_orders; /*customer demand*/
read data orders_costs into [product customer] c=revenue n=num_orders; /*customer-product demand*/
/* solve variable and model description */
/*matrix of supply and demand*/
var x{O,D} >= 0;
/*model objective*/
max total_revenue = sum{i in O, j in D}c[i,j]*x[i,j];
/*constraints*/
constraint supply{i in O}: sum{j in D}x[i,j]=a[i];
constraint demand{j in D}: sum{i in O}x[i,j] >= 0.1*b[j];
/* solve and output */
solve;
print x;
/* create data */
create data sparse from [customer product] x;
create data dense from [product]=O {j in D} <col(j)=x[product,j]>;
quit;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The demand constraint I proposed makes sure that at least 10% of each customer's total demand (summed across all products) is satisfied. Maybe you instead want the following, which forces at least 10% of each customer-product demand to be satisfied:
constraint demand{i in O, j in D}: x[i,j] >= 0.1*n[i,j];
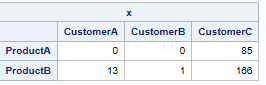
On my machine, the resulting optimal solution, with objective value 61500, is:
| x | |||
|---|---|---|---|
| CustomerA | CustomerB | CustomerC | |
| ProductA | 10 | 0 | 75 |
| ProductB | 13 | 1 | 166 |
In that case, you do not need b[j] and can omit the demand data set.
Alternatively, you can implicitly enforce these constraints by omitting the explicit demand constraint declaration and changing the lower bound on x:
var x{i in O, j in D} >= 0.1*n[i,j];
On my machine, the resulting optimal solution, with objective value 61500, is:
| x | |||
|---|---|---|---|
| CustomerA | CustomerB | CustomerC | |
| ProductA | 84 | 0 | 1 |
| ProductB | 173 | 1 | 6 |
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
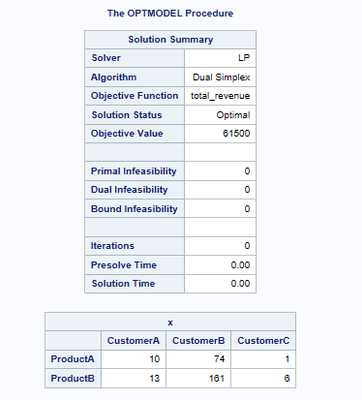
Thanks again for your effort on this, would you mind posting your full optmodel code? I'm getting the same objective value but not the same matrix of customers/products.
data orders_costs;
length customer $25. product $25. revenue 8. num_orders 8.;
input customer & product & revenue num_orders;
cards;
CustomerA ProductA 300 100
CustomerA ProductB 200 130
CustomerB ProductA 300 0
CustomerB ProductB 200 10
CustomerC ProductA 300 10
CustomerC ProductB 200 60
;
data supply;
length product $25. supply 8;
input product & supply;
cards;
ProductA 85
ProductB 180
;
proc optmodel;
/* declare sets and data indexed by sets */
set <str> O;
set <str> D;
number a{O};
number b{D};
number c{O,D};
number n{O,D};
/* read data */
read data supply into O=[product] a=supply; /*supply*/
read data orders_costs into D=[customer] b=num_orders; /*customer demand*/
read data orders_costs into [product customer] c=revenue n=num_orders; /*customer-product demand*/
/* solve variable and model description */
/*matrix of supply and demand*/
var x{O,D} >= 0;
/*model objective*/
max total_revenue = sum{i in O, j in D}c[i,j]*x[i,j];
/*constraints*/
constraint supply{i in O}: sum{j in D}x[i,j]=a[i];
constraint demand{i in O, j in D}: x[i,j] >= 0.1*n[i,j];
/* solve and output */
solve;
print x;
/* create data */
create data sparse from [customer product] x;
create data dense from [product]=O {j in D} <col(j)=x[product,j]>;
quit;Output:
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The code you showed is the same as what I ran. When there are alternative optimal solutions like in this case, different machines can yield different solutions. The solver considers them all equally desirable if they satisfy the constraints and have the same objective value. If you have a preference for one solution over another, that needs be captured in the optimization model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
That is interesting to know about the results being different on different machines but makes sense as long as the conditions are met.
I'm still a bit confused on what I have wrong with my constraints because the solver is providing results that are greater than my customer orders. For example, CustomerB ordered 10 of Product B but the solver is giving them 161.
Rob I have to again thank you for holding my hand on this, it's clear I do not fully understand this procedure but I'm planning on reading several of your papers this weekend.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
The current model does not impose any explicit upper bound on how many units of a product get sent to a customer. If you want to restrict to the number that were ordered, you can modify the demand constraint as follows:
constraint demand{i in O, j in D}: 0.1*n[i,j] <= x[i,j] <= n[i,j];
Alternatively, you can impose the bounds in the variable declaration:
var x{i in O, j in D} >= 0.1*n[i,j] <= n[i,j];
With either change, CustomerB will get between 1 and 10 units of ProductB.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Brilliant! Thank you Rob!
April 27 – 30 | Gaylord Texan | Grapevine, Texas
Registration is open
Walk in ready to learn. Walk out ready to deliver. This is the data and AI conference you can't afford to miss.
Register now and save with the early bird rate—just $795!
- Discovery-based Investigation in SAS Visual Investigator – Your Guide to Better Searches | 20-Jan-2026
- SAS Bowl LVIII, SAS Viya Copilot | 21-Jan-2026
- Ask the Expert: Wie der SAS Visual Analytics Copilot Ihre Arbeit beschleunigt! | 22-Jan-2026
- Ask the Expert: The AI Advantage: How SAS Customer Intelligence 360 Solves Real Marketing Challenges | 27-Jan-2026
- DCSUG presents SAS OnDemand for Academics: the Easy Way to Learn SAS For Free for Students, Educator | 27-Jan-2026
- Ask the Expert: How to Supercharge Enterprise Agentic Workflows With SAS Retrieval Agent Manager | 05-Feb-2026
- Ask the Expert: Implementing a Digital Twin for the Monopoly Board Game Using SAS® Viya® | 12-Feb-2026