- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I have code in proc optmodel that outputs a solution to a minimization problem. The solution matrix is a binary matrix which represents a column choice of restaurants szone value that best matches the ID's (first column s 1,2,3...) szone value. The following SAS code is where I am now.
data WORK.RestaurantsBySzone;
Infile datalines delimiter="#";
length Restaurant $100.;
input Restaurant $ szone;
datalines;
McDonalds#1
Subway#1
Tim Hortons#1
Starbucks#1
KFC#2
Wendys#2
Taco Bell#2
Pizza Hut#2
Ruby Tuesday#3
Whataburger#3
Burger King#3
IHOP#3
;
run;
data WORK.OPEN_F1_FINAL;
Infile datalines delimiter='#';
input
S
szone
Var1
Var2
Var3
;
datalines;
1#3#2#2#3
2#1#2#3#3
3#2#2#1#1
4#2#3#1#3
5#3#1#1#2
6#1#3#1#3
7#2#3#1#1
8#3#3#3#1
9#1#3#2#2
10#2#1#2#2
11#2#3#2#6
12#2#2#2#2
13#2#2#2#1
14#1#2#1#3
15#1#1#2#3
16#3#2#2#1
17#3#1#1#3
18#1#1#3#1
19#1#3#2#3
20#1#3#1#3
;
Run;
data WORK.CoorespondingRestaurants;
Length
Var1 $100.
Var2 $100.
Var3 $100.;
Infile datalines delimiter='#';
input
S
szone
Var1 $
Var2 $
Var3 $
;
datalines;
1#3#Pizza Hut#KFC#Ruby Tuesday
2#1#Pizza Hut#IHOP#Whataburger
3#2#Taco Bell#McDonalds#Subway
4#2#Burger King#McDonalds#Ruby Tuesday
5#3#Starbucks#Tim Hortons#Taco Bell
6#1#Whataburger#Subway#Burger King
7#2#Burger King#Subway#Tim Hortons
8#3#IHOP#Whataburger#Starbucks
9#1#IHOP#Pizza Hut#KFC
10#2#Starbucks#Pizza Hut#KFC
11#2#IHOP#Wendys#
12#2#Pizza Hut#Wendys#Taco Bell
13#2#Taco Bell#KFC#Tim Hortons
14#1#Pizza Hut#Subway#Ruby Tuesday
15#1#Starbucks#Taco Bell#Burger King
16#3#Pizza Hut#KFC#Starbucks
17#3#Starbucks#Subway#Whataburger
18#1#McDonalds#Burger King#Starbucks
19#1#Whataburger#Wendys#Burger King
20#1#Whataburger#Subway#IHOP
;
Run;
PROC SQL;
CREATE TABLE WORK.CoorespondingRestaurants AS
SELECT t1.S,
t1.szone,
t1.Var1,
t1.Var2,
t1.Var3
FROM WORK.COORESPONDINGRESTAURANTS t1;
QUIT;
proc optmodel;
ods output PrintTable#4=F1_Solution;
set SSET;
set JSET = 1..3;
num a {SSET, JSET};
num szone {SSET};
read data OPEN_F1_FINAL into SSET=[s] {j in JSET} <a[s,j] = col('Var'||(j))> szone;
var X {SSET, JSET} binary;
var Abs {SSET};
min Objective = (sum {s in SSET} Abs[s]) / (sum {s in SSET} szone[s]);
constraint OnceChoice {s in SSET}: sum {j in JSET} X[s,j] = 1;
constraint AbsCon1 {s in SSET}: Abs[s] >= sum {j in JSET} a[s,j]*X[s,j] - szone[s];
constraint AbsCon2 {s in SSET}: Abs[s] >= -sum {j in JSET} a[s,j]*X[s,j] + szone[s];
solve;
print a szone;
print Objective;
print X;
quit;
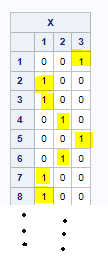
the solution matrix:
can be translated to: for S = 1 the best matched restaurant is 'Ruby Tuesday', and so forth for the other rows which can be determined by pairing the corresponding column with a 1 to the COORESPONDINGRESTAURANTS table.
The subproblem is that I want to apply a limitation to how many of each restaurant can be chosen during the optimization. i.e I don't want the optimizer to choose McDonalds or KFC more often than another restaurant of the same szone based on the rule that
an szone 1 restaurant can only be chosen at most once in the solution
an szone 2 restaurant can only be chosen 2 times in the solution
an szone 3 restaurant can only be chosed at most 2 times in the solution.
There are 3 szones and 4 restaurants in each szone as shown in the table RESTAURANTBYSZONE.
in excel, I would count using countifs or something the number of time a restaurant has been chosen and compare that to my szone rules:
| szone | numof choices in solution | comment | |
| McDonalds | 1 | 2 | WRONG - too many |
| Subway | 1 | 3 | WRONG - too many |
| Tim Hortons | 1 | 0 | OK |
| Starbucks | 1 | 1 | OK |
| KFC | 2 | 2 | OK |
| Wendys | 2 | 2 | OK |
| Taco Bell | 2 | 4 | WRONG - too many |
| Pizza Hut | 2 | 2 | OK |
| Ruby Tuesday | 3 | 1 | OK |
| Whataburger | 3 | 1 | OK |
| Burger King | 3 | 1 | OK |
| IHOP | 3 | 1 | OK |
on lines 2 and 3 above) Perhaps the optimizer could have chosen Tim Hortons instead of Subway when it had the choice of szone 1's. How does this correspond to a subproblem in my current proc optmodel?
Thanks so much!
- Tags:
- proc optmodel
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Sorry for the false start, which I have now deleted.
You can omit the PROC SQL call, which doesn't change anything.
Add this DATA step:
data szoneData;
input szone szoneLimit;
datalines;
1 1
2 2
3 2
;
Then add these OPTMODEL statements before the solver call:
set <str> RESTAURANTS;
num szone_r {RESTAURANTS};
read data RestaurantsBySzone into RESTAURANTS=[Restaurant] szone_r=szone;
str restaurant_sj {SSET, JSET};
read data CoorespondingRestaurants into [s] {j in JSET} <restaurant_sj[s,j] = col('Var'||(j))>;
set SZONES;
num szoneLimit {SZONES};
read data szoneData into SZONES=[szone] szoneLimit;
con SzoneCon {r in RESTAURANTS}:
sum {s in SSET, j in JSET: restaurant_sj[s,j] = r} X[s,j] <= szoneLimit[szone_r[r]];After the solve, you can verify that the new constraint is satisfied by adding this statement:
print SzoneCon.body SzoneCon.ub;On my machine, the results are:
| [1] | SzoneCon.BODY | SzoneCon.UB |
|---|---|---|
| Burger King | 2 | 2 |
| IHOP | 2 | 2 |
| KFC | 2 | 2 |
| McDonalds | 1 | 1 |
| Pizza Hut | 2 | 2 |
| Ruby Tuesday | 2 | 2 |
| Starbucks | 1 | 1 |
| Subway | 1 | 1 |
| Taco Bell | 2 | 2 |
| Tim Hortons | 1 | 1 |
| Wendys | 2 | 2 |
| Whataburger | 2 | 2 |
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
so, I may be misunderstanding how this works.
The values in the soluion Matrix X[s,j] are just the binary matrix of values which correspond to the szone choice in matrix a? It appears that this solution assumes that the columns in X correspond to szones? when the columns in X are just representative of the variable order in a. So I was trying to figure out how summing X[s,j] is counting the distinct restaurant choices as demonstrated in the excel counting method as shown in the pic below.
I think I can visualize how the szonelimit[szone[s]] is working. Seems to be a lookup based on the limit matrix we defined earlier.
thanks Rob
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Sorry for the false start, which I have now deleted.
You can omit the PROC SQL call, which doesn't change anything.
Add this DATA step:
data szoneData;
input szone szoneLimit;
datalines;
1 1
2 2
3 2
;
Then add these OPTMODEL statements before the solver call:
set <str> RESTAURANTS;
num szone_r {RESTAURANTS};
read data RestaurantsBySzone into RESTAURANTS=[Restaurant] szone_r=szone;
str restaurant_sj {SSET, JSET};
read data CoorespondingRestaurants into [s] {j in JSET} <restaurant_sj[s,j] = col('Var'||(j))>;
set SZONES;
num szoneLimit {SZONES};
read data szoneData into SZONES=[szone] szoneLimit;
con SzoneCon {r in RESTAURANTS}:
sum {s in SSET, j in JSET: restaurant_sj[s,j] = r} X[s,j] <= szoneLimit[szone_r[r]];After the solve, you can verify that the new constraint is satisfied by adding this statement:
print SzoneCon.body SzoneCon.ub;On my machine, the results are:
| [1] | SzoneCon.BODY | SzoneCon.UB |
|---|---|---|
| Burger King | 2 | 2 |
| IHOP | 2 | 2 |
| KFC | 2 | 2 |
| McDonalds | 1 | 1 |
| Pizza Hut | 2 | 2 |
| Ruby Tuesday | 2 | 2 |
| Starbucks | 1 | 1 |
| Subway | 1 | 1 |
| Taco Bell | 2 | 2 |
| Tim Hortons | 1 | 1 |
| Wendys | 2 | 2 |
| Whataburger | 2 | 2 |
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
ok I see. the call for
sum {s in SSET, j in JSET: restaurant_sj[s,j] = r} X[s,j]
is equivalent to the COUNTIFS like in excel - taking the choice of Szone as indicated by X.
elegant solution. The problem becomes more fickle if I play with the limit per szone in the szonedata; but, this definitely answers the question.
Thanks Rob!
- Ask the Expert: The AI Advantage: How SAS Customer Intelligence 360 Solves Real Marketing Challenges | 27-Jan-2026
- DCSUG presents SAS OnDemand for Academics: the Easy Way to Learn SAS For Free for Students, Educator | 27-Jan-2026
- Ask the Expert: How to Supercharge Enterprise Agentic Workflows With SAS Retrieval Agent Manager | 05-Feb-2026
- Ask the Expert - Génération de données synthétiques : innovation et confidentialité | 10-Feb-2026
- Ask the Expert: Implementing a Digital Twin for the Monopoly Board Game Using SAS® Viya® | 12-Feb-2026
- SAS CI360 Tips and Tricks: Quick Wins, Shortcuts and Hidden Features Every Marketer Should Know | 17-Feb-2026
- SAS Bowl LIX, Integrating SAS and Git | 18-Feb-2026