Synergism, antagonism, additivity – coding partially crossed rate factors a mixed model context
Suppose you have two products and want to test their rate responses at two levels. You hypothesize that when the products are mixed, it changes their performance somehow. That is a test of additivity.
And you’re interested in testing the effects in a full factorial multi-rate context.
But when the summery ebullience of factorization crashes against the wintry headwinds of limited resources, it forces experiment designers to make hard choices.
So, rather than test the products together at both rates, you must pick one consistent rate to test them. Based on your domain expertise, you select the lower rate of the two together.
Our simulated experiment consists of salicylic acid (SA), which induces natural plant defenses against pests and diseases, and a fungicide, which targets the fungus directly. Your goal is to test the effects of these products on crop yield.
List of treatments as rates expressed in kilograms formulated product per hectare (kg ai/ha) are:
- Control (0 kg/ha)
- SA @ 0.5 kg/ha
- SA @ 1 kg/ha
- Fungicide @ 5 kg/ha
- Fungicide @ 10 kg/ha
- SA @ 0.5 kg/ha + Fungicide @ 5 kg/ha
The last treatment and the absence of SA + fungicide at the higher rates represents the “partially crossed rate factor”.
We initially assess the data in proc transreg.
proc transreg data=import2 ss2 plots=fit(nocli noclm);
ods output coef=coef;
model identity('Yield_(tonnes/ha)'n) = identity(SA_Rate) | class(Fung_Rate);
run;
Our interest is to test the SA + fungicide combination in three mutually exclusive hypotheses:
Antagonism – that SA and fungicide effect on yield improvement is less than either of the individual treatments.
Additive – that SA and fungicide effect on yield improvement are like if their effects were added together.
Synergism– that SA and fungicide effect on yield improvement is greater than if the individual treatments were added together.
Additivity is the null hypothesis – that SA won’t change the effect of fungicide, and conversely fungicide won’t change the effect of SA. Synergism and antagonism are the alternative hypotheses, either of which would be denoted by a significant p value in our two tailed test (antagonism would show a lower yield, and synergism a higher yield).
Meanwhile, we also want to discern the effects of the individual factors and model the response curves. Hence our model will test the following effects:
SA_Rate response (linear and quadratic)
Fung_Rate response (linear and quadratic)
SA_Rate*Fung_Rate (linear only, based on the partial factorial)
In a blocked-design mixed model context, with the random factor replicate, it can be coded like this:
proc mixed data=work.import2 CL=WALD plots=all;
class 'Rep.'n Fungicide SA;
model 'Yield_(tonnes/ha)'n= SA_Rate|Fung_Rate SA_Rate*SA_Rate Fung_Rate*Fung_Rate /s htype=3 covb outp=out ddfm=kr2;
random 'Rep.'n / solution;
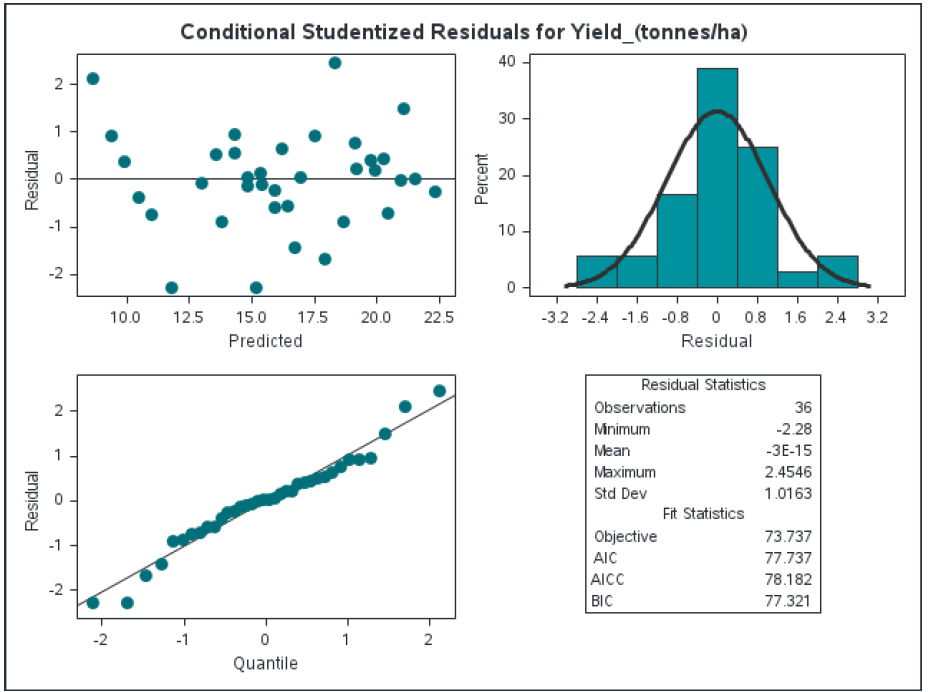
run;The residual plots look reasonable. Although there are some outliers (probably worth checking), the distribution is relatively normal and homoscedastic.
We also check the covariance parameter estimates to see how much unexplained variation there was. For a field trial, the residual variation was relatively low relative to the effect of the replicate.
Finally, we see the solution for fixed effects. We see that SA_Rate and Fung_Rate showed positive (for every one kg/ha fungicide applied, there is a 0.9135 kg/ha yield gain) and significant effects (p<0.0001). The quadratic rate response was significant for SA (negative value indicates a levelling off-effect), but not quite for fungicide (p=0.1214).
Most notably, the effect of SA_Rate*Fung_Rate was not significant (p=1.000) with an infinitesimally low estimate. This means that SA and Fungicide have no effect on each other whatsoever, at this rate. In the context of the main effects, SA is good, Fungicide is good, and they are good (though not necessarily better) together.
