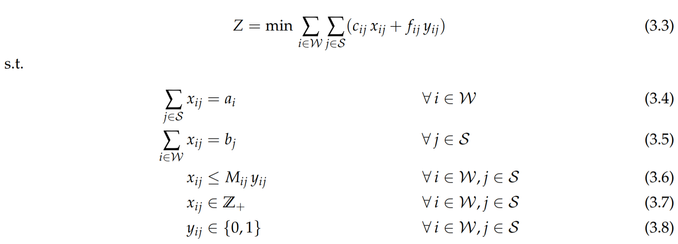Hackathon Highlights: How we used SAS AI to Optimize Shipping Logistics
1 - Introduction
A few months ago, @Lukkas, @ElifSaracoglu, @TerenceT3 and I participated in the SAS AI Hackathon, an internal SAS competition among associates in the Global Customer Advisory Academy. During this competition, we had the opportunity to first learn and explore SAS AI technologies, and then to build a creative application of our own to solve a real-life business problem.
Our team decided to tackle an optimization problem in just a day and a half for our hackathon project. We designed an application to support companies in the transportation and logistics industries, but the technology can be extended and applied to any industry that requires the movement of product between locations, such as the retail or manufacturing industries. We focused on 
Optimization refers to finding the optimal (i.e. best/most effective) value to maximize or minimize a certain objective function, subject to certain conditions or constraints. In this case, we are looking to minimize total transportation cost, whilst meeting all forecasted demand.
2 - The Business Problem: Making Shipping Logistics More Logical
For our hackathon project, we decided to optimize shipping logistics for a fictitious logistics company based in North Carolina. The company currently uses manual route planning: Each warehouse has a floor manager, and once a week, this manager forecasts quantities to be shipped to each store from his specific warehouse the following week. The floor managers base their estimates on current demand, doing a few calculations on an Excel spreadsheet to see how many units were sold in the previous week. If a store runs out of product during the week, an order will be sent to the warehouse, and these items will be shipped to the store immediately, which means a vehicle is carrying just that order to the store, resulting in very high total transportation costs.
It is important to note that the store managers do not collaborate with one another, and currently all warehouses supply to all stores, regardless of distance between locations.
How can the company find the optimal routes to take, as well as the optimal quantities to ship? What if some stores can get all their goods from just one or two warehouses, instead of all of them?
Here is a brief summary of the company’s goal, the current problems it must overcome, and the capabilities of the solution we set out to create:
Goal:
To minimize total transportation costs of shipping goods from warehouses to stores, whilst meeting all forecasted customer demand.
Current problems:
• Transportation routes and quantities of goods transported are currently not optimized.
• Weekly manual route planning is done in Excel by the coordinator of each individual warehouse.
• Coordinators do not communicate with one another.
• Route planning takes too long, so it is only done on a weekly basis.
• No mathematical modeling is used to help deduce the most efficient and cost-reducing routes and destinations automatically.
What capabilities does the solution need?
• Automatically identify the optimal route and amount of goods to be shipped from each warehouse to each store.
• Easily plan routes daily/hourly – so that if changes in demand occur, the shipping routes and quantities can be quickly updated and put into effect.
• Adapt to changes quickly.
• Coordinate trucks at a company-wide level and not the current warehouse level.
• Optimize routes and quantities to always satisfy the level of demand.
The optimization problem, which is defined below, aims to solve this problem of automatically calculating the optimal routes and the quantities required to be transported, ultimately satisfying forecasted demand and minimizing transportation costs.
3 - Defining the Optimization Problem
The shipping logistics problem explained above has the same structure as the classical fixed charge transportation problem (FCTP) and can be solved as a mixed integer linear program (MILP), minimizing the total shipping costs.
3.1 Mathematical model formulation
The FCTP is a generalization of the regular transportation problem, where an additional fixed cost is triggered if a route is established between a source node (warehouse, in our case) and a sink node (retail store). In the FCTP, the total transportation cost is minimized by deciding both which routes should be established and how much should be sent on these routes. Thus, in the FCTP we are given a set of source nodes representing the warehouses W indexed by i ∈ W = {1, ..., n}, and a set of sink nodes representing the stores S indexed by j ∈ S = {1, ..., m}. If a warehouse i ∈ W supplies goods to a store j ∈ S, a fixed cost fᵢⱼ is triggered to establish the connection. For each unit sent from a warehouse i to a store j, a cost cᵢⱼ is triggered. Each warehouse i has aᵢ units available to be shipped, and each store j demands bⱼ units. A capital letter M is used to define how much can be shipped between a warehouse i and a store j, and is defined as Mᵢⱼ = min{aᵢ, bⱼ}. In order to formulate a mathematical model of the problem, two variables are introduced, xᵢⱼ and yᵢⱼ. The variable xᵢⱼ must be a positive integer and indicates how many units are sent from warehouse i to store j. The variable yᵢⱼ is binary and indicates if any connection is established between warehouse i and store j, and thereby triggers the fixed cost fᵢⱼ.
Minimizing the total shipping costs and assuming
the MILP of the FCTP is formulated as follows:
The objective defined in 3.3 minimizes the total shipping costs. Constraint 3.4 ensures that all units at each warehouse i are shipped. Constraint 3.5 ensures that all units demanded at each store j are received. Constraint 3.6 defines the maximum number of units to be sent from warehouse i to store j.
3.2 Solution example
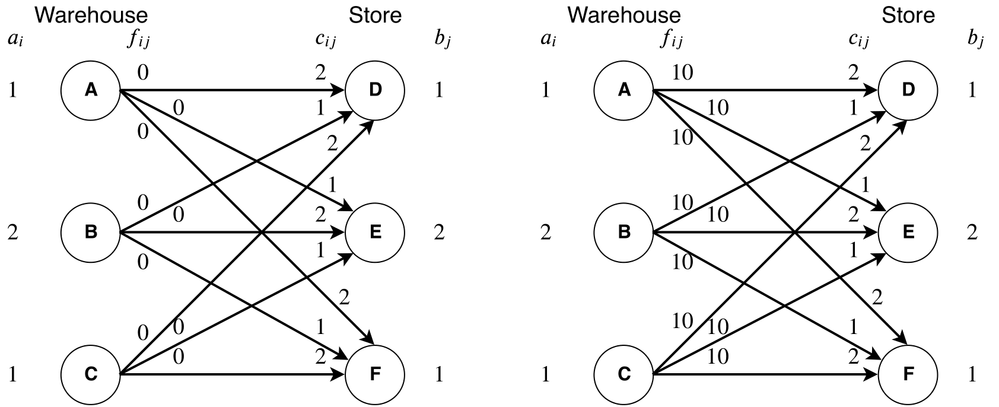
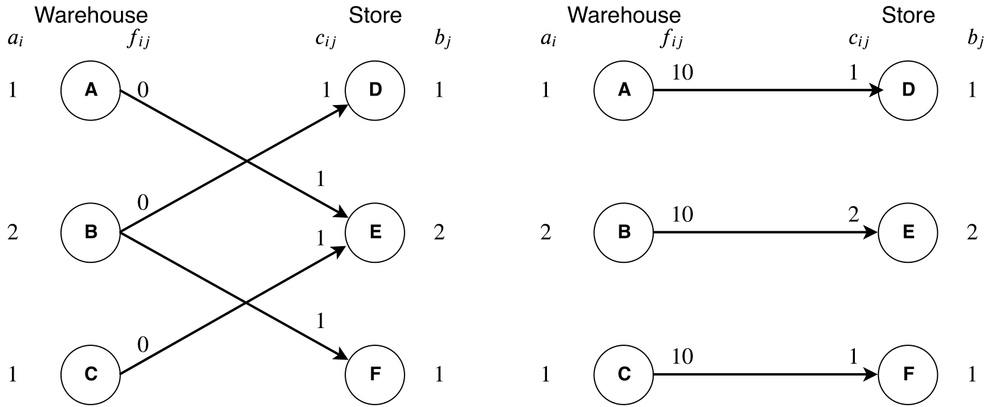
In the following figure, two simple examples of solutions are given to serve as an illustration.
First, two instances are assumed, each having three warehouses (A, B, C) that may ship goods to three stores (D, E, F). Each of the two instances has similar parameters, except for the assumed fixed costs fᵢⱼ. The two instances are presented in Figure 1 along with all associated parameters.
4 - Building our Solution, Using the Power of SAS and Open Source
To build our AI application for the business, the mathematical model presented in subsection 3.1 was implemented in Python utilizing a combination of standard Python packages and SAS packages. In the following section, the Python code implemented in a Jupyter Notebook is presented.
4.1 Packages
First, the packages needed are imported. The swat and the sasoptpy packages were developed by SAS, allowing users to code in Python syntax while leveraging the power of SAS. The swat package makes it possible to connect to the SAS Cloud Analytic Services (CAS) engine in SAS Viya and utilize the in-memory distributed engine, and the sasoptpy package makes it possible to model the optimization problem as an MILP that can be processed in CAS. The two other packages used are the two standard Python packages pandas and numpy.
# SAS packages
import swat
import sasoptpy as so
# Python packages
import pandas as pd
import numpy as np
4.2 Connecting to CAS
Here we utilize the swat package to establish a connection to the CAS server.
# connecting to cas
cas_conn = swat.CAS(hostname=server, port=port,
,protocol="http", username=name, password=key)
4.3 Importing Data
Here we import, clean and prepare the data for modelling using both pandas and numpy.
# importing data
df = pd.read_csv("Data\\instanceA.csv", sep=";")
a = pd.DataFrame(list(df["a"]), columns=["a"])
a = a[a['a'] != 0]
b = pd.DataFrame(list(df["b"]), columns=["b"])
b = b[b['b'] != 0]
c_s = df["c"].str.split("}", n = 1, expand = True)[1].apply(lambda x: x.
,!strip("[").strip("]"))
c = c_s.str.split(',', expand=True).dropna()
5
f_s = df["f"].str.split("}", n = 1, expand = True)[1].apply(lambda x: x.
,!strip("[").strip("]"))
f = f_s.str.split(',', expand=True).dropna()
I = a["a"].shape[0]
J = b["b"].shape[0]
warehouse_list = [i for i in range(1, I+1)]
store_list = [j for j in range(1, J+1)]
indx = pd.Series(warehouse_list)
a = a.set_index(indx)
indx = pd.Series(store_list)
b = b.set_index(indx)
cost_per_unit = pd.DataFrame(
np.matrix(c), columns=store_list, index=warehouse_list).astype(float)
fixed_cost = pd.DataFrame(
np.matrix(f), columns=store_list, index=warehouse_list).astype(float)
# big M
ub = np.zeros((I,J))
for i in range(1, I+1):
for j in range(1, J+1):
ub[i-1,j-1] = min(a.at[i, "a"], b.at[j, "b"])
ub = pd.DataFrame(ub, columns=store_list, index=warehouse_list)
4.4 Defining and Solving FCTP
Finally, we define the model using the sasoptpy package and solve it in CAS using the connection established through the swat package. In the very end, the output is printed showing the cost of the optimal solution and the decision variables for the instance solved.
def fctp(warehouse_list, store_list, cost_per_unit, fixed_cost, i, j, a, b):
# model
m = so.Model(name='FCTP', session=cas_conn)
# variables
x = m.add_variables(warehouse_list, store_list, vartype = so.INT,
,name='Amount')
y = m.add_variables(warehouse_list, store_list, vartype = so.BIN,
,name='Route')
# objective
fixed_cost_obj = so.quick_sum(fixed_cost.at[i, j] * y[i, j] for i in
,warehouse_list for j in store_list)
cost_per_unit_obj = so.quick_sum(cost_per_unit.at[i, j] * x[i, j] for i in
,warehouse_list for j in store_list)
m.set_objective(cost_per_unit_obj + fixed_cost_obj, sense=so.MIN,
,name='total_cost')
# c1
m.add_constraints((so.quick_sum(x[i, j] for j in store_list) == a.at[i,"a"]
,for i in warehouse_list), name='inventory')
# c2
m.add_constraints((so.quick_sum(x[i, j] for i in warehouse_list) == b.
,at[j,"b"] for j in store_list), name='demand')
# c3
m.add_constraints((x[i, j] <= ub.at[i,j] * y[i, j] for i in warehouse_list
,for j in store_list), name='max_flow')
# solve
result = m.solve({'with': 'milp', 'maxtime': 5})
return m.get_objective_value(), so.get_solution_table(x, y)
obj_value, variables = fctp(warehouse_list, store_list, cost_per_unit,
,fixed_cost, i, j, a, b)
print("")
print("Objective value", obj_value)
print("")
print("Variables \n", variables)*For full results from the code, kindly consult the attached PDF to see each iteration.
The optimal value from this code was: 18284.
This means that the minimum cost of transportation for this specific problem yields to be $18,284.00.
The code also generated a routing table to assist in showing which warehouses should serve which stores. The results of these were presented in SAS Visual Analytics on SAS Viya.
4.5 Integration in SAS Viya
Finally, with our model created and an optimized solution found, it is time to create a skin for the application, which allows the business users - in our case, warehouse coordinators - to easily access the information they need to derive value. For our project, the user is initially provided with the following web interface:
The results are presented to the user in SAS Visual Analytics on Viya:
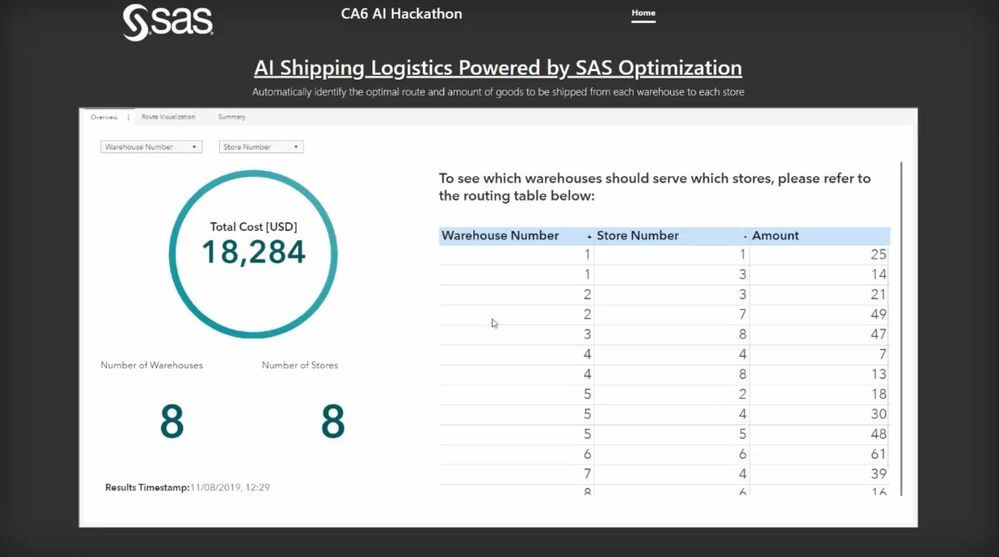
As seen in the image above, the resulting dashboard shows the optimal cost, i.e. the minimum total cost, as well as the routing table, which lists the quantity that each store should receive from each warehouse. These results will always satisfy the total demand that was provided in the input data file. It also lists the number of stores and warehouses that were uploaded to the optimization problem. In this case, we have eight warehouses supplying eight stores, and if they ship the optimal amounts of product listed in the far right column, total cost to the company will be minimized at $18, 284. The user will then be able to filter the results accordingly to view the relevant warehouse and prepare the goods to be shipped from that warehouse.
In summary:
• The manual route planning is no longer needed.
• Optimal routes and quantities are automatically identified.
• The route planning can be done more frequently and adjusted as changes occur.
• This solution is applied at a company-wide level and not just a warehouse-level.
• The results show the minimum total cost to the company that satisfies total customer demand.
5 - Interested in Learning More?
Please feel free to contact any of us if you have any questions or want to find out more about our solution!
This was a wonderful opportunity to explore what is capable with SAS, and how open source capabilities can also be implemented to form one cohesive solution. Our team would like to thank the Customer Advisory Academy and the AI Hackathon team for taking the time to teach us more about AI techniques, inspiring us to tackle this problem and build a better business solution.
