- Home
- /
- Analytics
- /
- Stat Procs
- /
- Zero-Inflated Gamma Model - NLMIXED - SAS 9.4
- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Dear All,
I am tring to model a zero inflated log-gamma model in a multicenter study. I have a semicontinuous outcome which is gamma distributed for the non-zero part of the distribution. However around 20% of patients scored zero for the outcome variable.
I initially modelled 1 independent variable (country) in a fixed effect model just to check whether I could do the coding right. I dummy coded this variable (which has 11 levels). I have got this warning:
Convergence criterion (GCONV=1E-8) satisfied.
NOTE: At least one element of the gradient is greater than 1e-3.
NOTE: Moore-Penrose inverse is used in covariance matrix.
WARNING: The final Hessian matrix is not positive definite, and therefore the estimated covariance
matrix is not full rank and may be unreliable. The variance of some parameter estimates is
zero or some parameters are linearly related to other parameters.
This is my code:
proc nlmixed data = data lognote = 3 ;
parms
/*intercept*/a0=1
/*country dummies - Sp is reference*/a1=0.1 a2=0.1 a3=0.1 a4=0.1 a5=0.1 a6=0.1 a7=0.1 a8=0.1 a9=0.1 /*a10=0.1*/ a11=0.1
log_theta = 0;
title "NLMIXED - Log-Gamma inflated model" ;
y = outcome;
linfp = a0 + a1*CZ + a2*FR + a3*HU + a4*IT + a5*PL + a6*PT + a7*RO + a8*RU + a9*SK + /*a10*SP + */a11*TR;
infprob = exp(linfp)/(1+exp(linfp)) ;
linp = b0 + b1*CZ + b2*FR + b3*HU + b4*IT + b5*PL + b6*PT + b7*RO + b8*RU + b9*SK + /*b10*SP +*/ b11*TR;
mu = exp(linp);
theta = exp(log_theta) ;
r = mu/theta ;
if y = 0 then ll = log(infprob) ;
else ll = log(1-infprob) - lgamma(theta) + (theta-1)*log(y) - theta*log(r) - y/r ;
model y ~ general(ll);
predict pred out=prediction;
run;
I am new to NLMIXED and I most likely did wrong somewhere. I would really appreciate if you could help me through.
Many thanks,
L.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I think your code is probably OK--the problem most likely is in the data, and how much you have. It looks like (at least to me) that you have nearly identical observations for at least 2 countries. This would lead to the degenerate condition that would throw the warning. What does the crosstab for y by country look like? It may be hard to get at if you have lots of data.
On the complete other hand, with 11 levels in a ZI model, you are estimating 20 fixed effects (captured in mu) plus theta, so the other possibility is not enough data to estimate all of the parameters well. So, if you only have a dozen or so patients per country, many of which have the same y value, you might be in this predicament.
Steve Denham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Dear Steve,
thanks for your reply. I have a very large sample (n range from 5K to 32K for each country). So the hypothesis of being underpowered seems very unlikely. I have looked at the y distributions in each country. Both the average and the % of zeros is different across countries. In one or two countries the % of zero is not so big while in some other countries the % of zero is very big. There seem not to be overlap between countries that would justify the warning.
I tried to run a similar model using proc FMM.
title "Finite Mixture Model - Gamma, zero inflated model" ;
proc fmm data =[DATA] gconv=0;
class country; model Y=country/dist=gamma ;
model Y=/dist=constant ;
probmodel country;
run;
The model failed to compute the mixing probabilities
This was not the case after running a zero inflated, log-normal model.
title "Finite Mixture Model - Lognormal, zero inflated model" ;
proc fmm data =[DATA] gconv=0;
class country; model Y=country/dist=Lognormal;
model Y=/dist=constant ;
probmodel country;
run;
The logs were the same for both models:
NOTE: Convergence criterion (FCONV=2.220446E-16) satisfied.
NOTE: At least one element of the gradient is greater than 1e-3.
NOTE: PROCEDURE FMM used (Total process time):
real time 5.43 seconds
cpu time 19.15 seconds
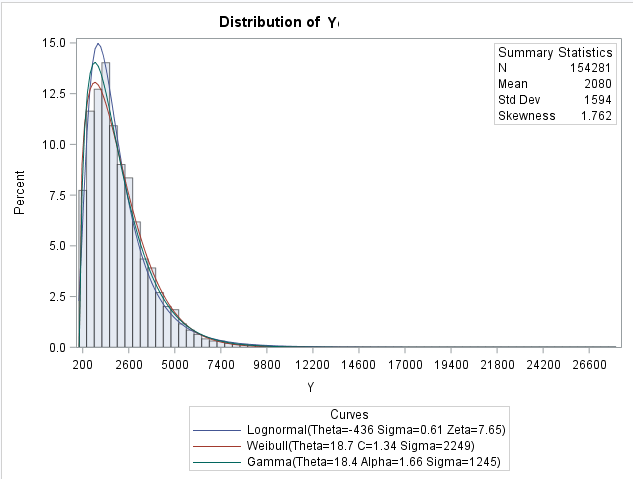
This is strange because, I looked at the distributions of the Y using proc univariate and the gamma distribution fitted the positive part of the Y distribution quite well (at least as well as the lognormal, in any case).
proc univariate data=[DATA];
var Y;
histogram Y/ midpoints=uniform
lognormal (theta=est)
weibull (theta=est)
gamma (theta=est)
vaxis = axis1
name = 'Histogram';
inset n mean(5.3) std='Std Dev'(5.3) skewness(5.3)
/ pos = ne header = 'Summary Statistics';
axis1 label=(a=90 r=0);
where Y ne 0;
run;
Any thought?
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
You could consider modifying the gamma deviance a bit as follows and fitting the model in GENMOD. This avoids the issue of GENMOD not allowing zero responses.
proc genmod;
d = _resp_/_mean_ + log(_mean_);
variance var = _mean_**2;
deviance dev = d;
model y = x / link = log;
run;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi Dave, Thanks for your reply. I know the modification you suggested and used it in the past. Actually I need to estimate a zero-inflated model bacause the gamma regression itself do not adequately fit the data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
I hate to start out with a bad pun, but what we need is a 'mix' of @StatDave ' s restatement of the gamma distribution that has support at zero and a whole boatload of zeroes in PROC FMM. I think the reason the lognormal gives mixing probabilities and the gamma doesn't there is due to the undefined nature at zero of the gamma.
But, you can show that the lognormal is a special case of the gamma (or vice versa, maybe), because I had to do it on a midterm about 40 years ago. And given that, I think the FMM with the lognormal is very likely a good model for the mixing probabilities under a more general gamma distribution.
Steve Denham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
@SteveDenham you might be misremembering the relationship between gamma and lognormal. Although each has limiting cases that asymptotically approach the normal distibution, I believe that the two distributions are distinct for any finite parameter values. If you plot the skewness and kurtosis of these distributions on a moment-ratio diagram, the curves do not overlap or intersect..
If you have my book Simulating Data with SAS, you can view a moment-ratio diagram in Chapter 16, such as Fig 16.3 or 16.9. I also have an online version of an appendix (p. 372) that contains a simplified moment-ratio diagram.
From a modeling perspective, however, the two distributions have similar shapes, which is the crux of your argument, I think.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks,@Rick_SAS.. The midterm probably was more like show that there is a special case of the gamma distribution that is identical to the chi-squared distribution--another asymmetric, long right tailed distribution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Ah yes, that makes sense.
Slightly off-topic, but have you ever wondered why some continuous distributions (like gamma) are supported by SAS procedures like PROC UNIVARIATE whereas others (like chi-square) are not? Maybe this was discussed in your theory classes, but exercises like you describe on your midterm muddy the water between distributions that describe data and distributions that describe statistics. For some philosophical musings on the matter (including the answer to your midterm exam question!), see "Why doesn't PROC UNIVARIATE support certain common distributions?"
SAS Innovate 2025: Call for Content
Are you ready for the spotlight? We're accepting content ideas for SAS Innovate 2025 to be held May 6-9 in Orlando, FL. The call is open until September 16. Read more here about why you should contribute and what is in it for you!
ANOVA, or Analysis Of Variance, is used to compare the averages or means of two or more populations to better understand how they differ. Watch this tutorial for more.
Find more tutorials on the SAS Users YouTube channel.