- RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Hi everyone,
I am new to IML and permutation tests. I'm working on a permutation test for repeated measures ANOVA. Below is code to
create a sample dataset and IML code to run the permutation test.
My questions...
Am I totally off base with this?
Could I better vectorize the computations?
Any comments on the appropriateness of this method?
Any comments on whether or not it could be used with count data?
Many thanks,
John
/* create test dataset */
data test;
input t1-t3;
datalines;
45 50 55
42 42 45
36 41 43
39 35 40
51 55 59
44 49 56
;;
run;
proc iml;
use test;
read all into xobt;
close test;
/* module to calculate F ratio */
start fmod;
gmean = x[:]; /* grand mean */
n = nrow(x); /* number of rows/subjects */
k = ncol(x); /* number of columns/treatments */
tmeans = x[:,]; /* treatment means */
submeans = x[,:]; /* subject means */
/* SSb */
SSb = (tmeans-gmean)##2;
SSb = n*(SSb[+]);
/* SSw */
SSw = (tmeans-x)##2;
SSw = SSw[+,];
SSw = SSw[+];
/* SSsub */
SSsub = k*((submeans-gmean)##2);
SSsub = SSsub[+];
SSerror = SSw-SSsub; /* SSerror */
MSt = SSb/(k-1); /* MSt */
MSerror = SSerror/((n-1)*(k-1)); /* MSerror */
F = MSt/MSerror; /* F statistic */
finish;
/* calculate F for observed data */
x = xobt;
run fmod;
fobt = F;
print fobt;
/* permutation test */
call randseed(1234);
x = j(nrow(xobt),ncol(xobt)); /* allocate matrix for permuted data */
B = 1000; /* number or reps */
fdist = j(B,1); /* vector to hold bootstrap dist of F */
do j = 1 to B; /* bootstrap loop */
/* permute each row */
do i = 1 to n;
p = xobt;
q = ranperm(p[i,]);
x[i,] = q;
end;
run fmod; /* calculate F on permuted data */
fdist[j,] = F; /* store calculated F in fdist vector */
end;
/* compute p-value */
pval = sum(fdist > abs(fobt)) / B;
print pval;
/* create dataset */
create bootf var {fdist};
append;
close bootf;
quit;
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
First, welcome to the world of SAS/IML programming! You might be interested in these tips for beginners. I write a blog about statistical programming in SAS, and many of my posts are "Getting Started Examples."
Second, you seem to be an excellent programmer. Your code is pretty good already, and you've clearly researched the problem and figured out the basics of the IML language. I think you'll be an expert who answers OTHER people's questions before long!
Here are some hints and suggestions that I think would improve the program:
1) Turn the FMOD module into a function with a local symbol table. For example,
start fmod(x);
...
return(F);
finish;
2) Vectorizing the inner loop (do i=1 to n) is tricky because there isn't a built-in SAS/IML function for "permute each row".
If your data sets are small, I would leave your code the way it is. Only if you are dealing with many rows (large n) will you want to improve the efficiency. If you are dealing with large n, or just want to learn more, read on. Otherwise, you're done.
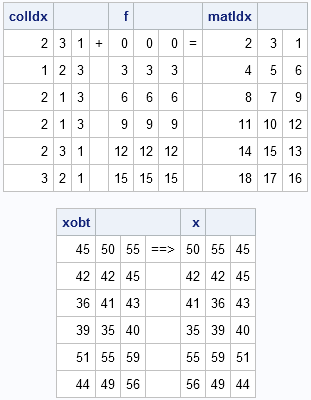
The RANPERM function supports a second argument that specifies the number of permutations to return. I would use this feature to vectorize the inner loop. Instead of permuting the ELEMENTS of p, permute the column indices {1 2 3}. You then need to convert the COLUMN indices into MATRIX indices by adding a constant that depends on the row. (See the article "Converting matrix subscripts to indices" for terminology and the computations.) I wrapped these ideas into the function PermuteWithinRows that you can call from within the bootstrap loop. I've attached output to illustrate the process.
proc iml;
use test; read all into xobt; close test;
/* independently permute elements of each row of a matrix */
start PermuteWithinRows(m);
colIdx = ranperm(1:ncol(m), nrow(m));
/* generate matrix indices */
f = (row(m) - 1) * ncol(m); /* ROW fcn in 12.3 */
matIdx = f + colIdx;
*print colIdx " + " f " = " matIdx;
return( shape(m[matIdx], nrow(m)) );
finish;
call randseed(1234);
x = PermuteWithinRows(xobt);
print xobt " ==> " x;
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
If I get some time I'll look at this more closely, but for now look at pp 11-14 of http://support.sas.com/resources/papers/proceedings10/329-2010.pdf to see an example of a matched pair permutation test. Not exactly what you are doing here, but some of the ideas might be helpful.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks, Rick! My apologies. I should have mentioned in the original post that your paper was my starting point. I used the ranperm function instead of the randgen as in the paper to permute the rows of the matrix.
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
First, welcome to the world of SAS/IML programming! You might be interested in these tips for beginners. I write a blog about statistical programming in SAS, and many of my posts are "Getting Started Examples."
Second, you seem to be an excellent programmer. Your code is pretty good already, and you've clearly researched the problem and figured out the basics of the IML language. I think you'll be an expert who answers OTHER people's questions before long!
Here are some hints and suggestions that I think would improve the program:
1) Turn the FMOD module into a function with a local symbol table. For example,
start fmod(x);
...
return(F);
finish;
2) Vectorizing the inner loop (do i=1 to n) is tricky because there isn't a built-in SAS/IML function for "permute each row".
If your data sets are small, I would leave your code the way it is. Only if you are dealing with many rows (large n) will you want to improve the efficiency. If you are dealing with large n, or just want to learn more, read on. Otherwise, you're done.
The RANPERM function supports a second argument that specifies the number of permutations to return. I would use this feature to vectorize the inner loop. Instead of permuting the ELEMENTS of p, permute the column indices {1 2 3}. You then need to convert the COLUMN indices into MATRIX indices by adding a constant that depends on the row. (See the article "Converting matrix subscripts to indices" for terminology and the computations.) I wrapped these ideas into the function PermuteWithinRows that you can call from within the bootstrap loop. I've attached output to illustrate the process.
proc iml;
use test; read all into xobt; close test;
/* independently permute elements of each row of a matrix */
start PermuteWithinRows(m);
colIdx = ranperm(1:ncol(m), nrow(m));
/* generate matrix indices */
f = (row(m) - 1) * ncol(m); /* ROW fcn in 12.3 */
matIdx = f + colIdx;
*print colIdx " + " f " = " matIdx;
return( shape(m[matIdx], nrow(m)) );
finish;
call randseed(1234);
x = PermuteWithinRows(xobt);
print xobt " ==> " x;

- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Thanks so much! This is super helpful. Converting the module to a function and using matrix indices definitely improved the performance. The actual data to be used will likely have around 150 rows so I will apply your techniques.
Thanks also for your encouragement and the link to the "Getting Started Examples". Much appreciated!
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
This is sweet--it addresses a nagging problem I have had with the permutations in a hierarchical design problem as well.
Steve Denham
- Mark as New
- Bookmark
- Subscribe
- Mute
- RSS Feed
- Permalink
- Report Inappropriate Content
Here's a blog post that I wrote about this problem:

Register Today!
Join us for SAS Innovate 2025, our biggest and most exciting global event of the year, in Orlando, FL, from May 6-9. Sign up by March 14 for just $795.
Learn how to run multiple linear regression models with and without interactions, presented by SAS user Alex Chaplin.
Find more tutorials on the SAS Users YouTube channel.



